
分析 (1)直接利用二次根式乘法运算法则计算得出答案;
(2)直接利用二次根式乘法运算法则再结合绝对值的性质化简计算得出答案;
(3)直接化简二次根式得出答案;
(4)直接利用乘法公式计算得出答案.
解答 解:(1)$\sqrt{5}$×$\sqrt{\frac{9}{20}}$=$\sqrt{5×\frac{9}{20}}$=$\frac{3}{2}$;
(2)$\frac{{\sqrt{20}-\sqrt{45}}}{{\sqrt{5}}}$+|1+$\root{3}{-64}}$|
=2-3+4-1
=2;
(3)$\sqrt{18}$-4$\sqrt{\frac{1}{2}}$+$\sqrt{8}$
=3$\sqrt{2}$-2$\sqrt{2}$+2$\sqrt{2}$
=3$\sqrt{2}$;
(4)(2-$\sqrt{3}$)(2+$\sqrt{3}$)-(3-$\sqrt{2}$)2
=4-3-(9+2-6$\sqrt{2}$)
=-10+6$\sqrt{2}$.
点评 此题主要考查了实数运算,正确化简二次根式是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,AF是⊙O的直径,P是AF延长线上的一点,PD切O于点D,E是AF上一点,PD=PE,DE的延长线交O于点C,问CO与AF的关系是什么?为什么?
已知,如图,AF是⊙O的直径,P是AF延长线上的一点,PD切O于点D,E是AF上一点,PD=PE,DE的延长线交O于点C,问CO与AF的关系是什么?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A,B的坐标分别为(0,8),(-3,0),点P从点A出发,以2单位/秒的速度沿射线AO方向运动,同时点E从点B出发,以1单位/秒的速度沿射线BO方向运动,以PE为斜边构造Rt△PEC(字母按逆时针顺序),且EC=2PC,抛物线y=-2x2+bx+c经过点(0,4),(-1,-2),设运动时间为t秒.
如图,点A,B的坐标分别为(0,8),(-3,0),点P从点A出发,以2单位/秒的速度沿射线AO方向运动,同时点E从点B出发,以1单位/秒的速度沿射线BO方向运动,以PE为斜边构造Rt△PEC(字母按逆时针顺序),且EC=2PC,抛物线y=-2x2+bx+c经过点(0,4),(-1,-2),设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
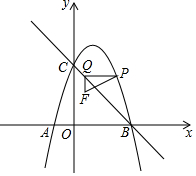 如图,在平面直角坐标系中,抛物线y=a(x-1)2+4与x轴交于点A、B两点,与y轴交于点C,且点B的坐标为(3,0),点P在这条抛物线的第一象限图象上运动.过点P作y轴的垂线与直线BC交于点Q,以PQ为边作Rt△PQF,使∠PQF=90°,点F在点Q的下方,且QF=1,设线段PQ的长度为d,点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=a(x-1)2+4与x轴交于点A、B两点,与y轴交于点C,且点B的坐标为(3,0),点P在这条抛物线的第一象限图象上运动.过点P作y轴的垂线与直线BC交于点Q,以PQ为边作Rt△PQF,使∠PQF=90°,点F在点Q的下方,且QF=1,设线段PQ的长度为d,点P的横坐标为m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com