
【题目】甲进行了10次射击训练,平均成绩为9环,且前9次的成绩(单位:环)依次为:8,10,9,10,7,9,10,8,10.
(1)求甲第10次的射击成绩;
(2)求甲这10次射击成绩的方差;
(3)乙在相同情况下也进行了10次射击训练,平均成绩为9环,方差为1.6环2,请问甲和乙哪个的射击成绩更稳定?
科目:初中数学 来源: 题型:
【题目】某专卖店有 A,B 两种商品.已知在打折前,买 20 件 A 商品和 10 件B 商品用了 400 元;买 30 件 A 商品和 20 件 B 商品用了 640 元.A,B 两种商品打相同折以后,某人买 100 件 A 商品和 200 件 B 商品一共比不打折少花 640 元,计算打了多少折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)【阅读发现】如图①,在△ABC中,∠ACB=45°,AD⊥BC于点D,E为AD上一点,且DE=BD,可知AB=CE.
(2)【类比探究】如图②,在正方形ABCD中,对角线AC与BD交于点O,E是OC上任意一点,AG⊥BE于点G,交BD于点F.判断AF与BE的数量关系,并加以证明.
(3)【推广应用】在图②中,若AB=4,BF= ![]() ,则△AGE的面积为 .
,则△AGE的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
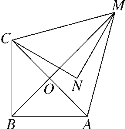
【题目】(题文)如图,在等腰直角三角形MNC中,CN=MN=![]() ,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
(1)∠NCO的度数为________;
(2)求证:△CAM为等边三角形;
(3)连接AN,求线段AN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组同学在一周内参加家务劳动时间与人数情况如下表所示:

下列关于“劳动时间”这组数据叙述正确的是( )
A. 中位数是2 B. 众数是2 C. 平均数是3 D. 方差是0
查看答案和解析>>
科目:初中数学 来源: 题型:
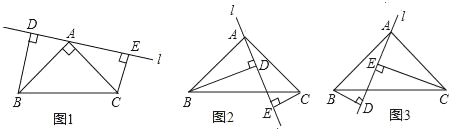
【题目】在△ABC中,∠BAC=90°,AB=AC,l是过A的一条直线,BD⊥AE于D,CE⊥AE于E.求证:
(1)当直线l绕点A旋转到如图1位置时,试说明:DE=BD+CE.
(2)若直线l绕点A旋转到如图2位置时,试说明:DE=BD﹣CE.
(3)若直线l绕点A旋转到如图3位置时,试问:BD与DE,CE具有怎样的等量关系?请写出结果,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
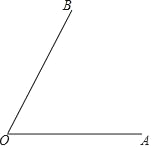
【题目】如图,∠AOB=60°,分别引射线OC、OD、OE,使OD平分∠BOC,OE平分∠AOD.
(1)若∠BOC=20°,请依题意补全图形,并求∠BOE的度数;
(2)若∠BOC=α(其中α是小于60°的锐角),请直接写出∠BOE的度数(用含α的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A坐标为(0,3),点B在x轴上 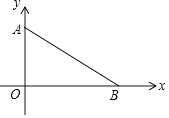
(1)在坐标系中求作一点M,使得点M到点A,点B和原点O这三点的距离相等,在图中保留作图痕迹,不写作法;
(2)若函数y= ![]() 的图象经过点M,且sin∠OAB=
的图象经过点M,且sin∠OAB= ![]() ,求k的值.
,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过点(0,﹣3),且顶点坐标为(﹣1,﹣4).
(1)求该二次函数的解析式;
(2)设该二次函数的图象与x轴的交点为A、B,与y轴的交点为C,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com