
分析 (1)根据整式的运算法则即可求出答案
(2)分式运算法则即可求出答案
解答 解:(1)原式=x2+4xy+y2-(4xy-4x2+y2-xy)
=8x2+xy,
(2)原式=[$\frac{3{y}^{2}}{x-y}$-$\frac{(x+y)(x-y)}{x-y}$]•$\frac{x(x-y)}{x(x-2y)}$
=$\frac{3{y}^{2}-{x}^{2}{+y}^{2}}{x-y}$•$\frac{x-y}{x-2y}$
=$\frac{-(x-2y)(x+2y)}{x-y}$•$\frac{x-y}{x-2y}$
=-x-2y
点评 本题考查的计算能力,解题的关键是熟练运用运算法则,本题属于基础题型.


 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
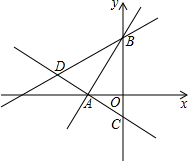 如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,∠ABO=30°,OB=3OC.
如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,∠ABO=30°,OB=3OC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 35×104 | B. | 350×103 | C. | 3.5×105 | D. | 0.35×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
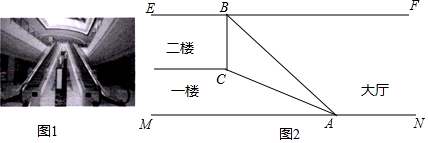
| A. | 3.6米 | B. | 4.9米 | C. | 4.1米 | D. | 5.2米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
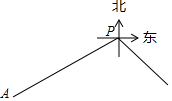 如图,甲船在港口P的南偏西60°方向,距港口86海里的A处,沿AP方向以每小时15海里的速度匀速行驶向港口P,乙船从港口P出发,沿南偏东45°方向匀速行驶驶离岗口P,现两船同时出发,2小时后乙船在甲船的正东方向,求乙船的航行速度(结果精确到个位,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)
如图,甲船在港口P的南偏西60°方向,距港口86海里的A处,沿AP方向以每小时15海里的速度匀速行驶向港口P,乙船从港口P出发,沿南偏东45°方向匀速行驶驶离岗口P,现两船同时出发,2小时后乙船在甲船的正东方向,求乙船的航行速度(结果精确到个位,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com