
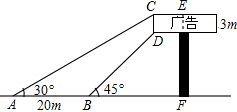
 如图,某广告牌竖直矗立在水平地面上,经测量得到如下相关数据:CD=3m,AB=20m,∠CAB=30°,∠DBF=45°,求广告牌的高EF(结果保留根号).
如图,某广告牌竖直矗立在水平地面上,经测量得到如下相关数据:CD=3m,AB=20m,∠CAB=30°,∠DBF=45°,求广告牌的高EF(结果保留根号). 分析 过点D作DG⊥AF于点G,设DG=xm,则CG=(x+3)m,解Rt△BGD,得出BG=DG=xm,则AG=BG+AB=(x+20)m.再解Rt△AGC,由tan30°=$\frac{GC}{AG}$,得出$\frac{x+2}{x+10}$=$\frac{\sqrt{3}}{3}$,解方程求出x的值,进而得出EF.
解答 解:如图,过点D作DG⊥AF于点G,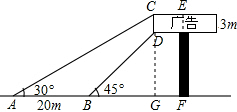 设DG=xm,则CG=(x+3)m.
设DG=xm,则CG=(x+3)m.
在Rt△BGD中,∵∠BGD=90°,∠DBG=45°,
∴BG=DG=xm,
∴AG=BG+AB=(x+20)m.
在Rt△AGC中,∵∠AGC=90°,∠CAG=30°,
∴tan30°=$\frac{GC}{AG}$,
∴$\frac{x+3}{x+20}$=$\frac{\sqrt{3}}{3}$,
∴x=$\frac{17\sqrt{3}+11}{2}$,
∴EF=CG=CD+DG=3+$\frac{17\sqrt{3}+11}{2}$=$\frac{17}{2}$$\sqrt{3}$+$\frac{17}{2}$(m).
答:广告牌的高EF为($\frac{17}{2}$$\sqrt{3}$+$\frac{17}{2}$)m.
点评 此题主要考查了解直角三角形的应用,根据已知构造直角三角形得出DG的长是解题的关键.


科目:初中数学 来源: 题型:选择题
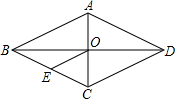 已知:如图,菱形ABCD对角线AC与BD相交于点O,E为BC的中点E,AD=6cm,则OE的长为( )
已知:如图,菱形ABCD对角线AC与BD相交于点O,E为BC的中点E,AD=6cm,则OE的长为( )| A. | 6cm | B. | 4cm | C. | 3cm | D. | 2cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
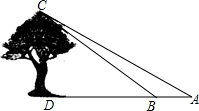 大庄中学9年级学生在学习“解直角三角形”一章时,开展测量物体高度的实践活动,他们要测量校园内一棵大树的高度.如图,在大树前的平地上选一点A,测得由点A看大树顶端C的仰角为35°,在点A和大树之间选择一点B(A,B,D在同一直线上),测得由点B看大树顶端C的仰角为45°,再量得A,B两点间的距离为5.43米,求大树CD的高度(结果精确到0.1米).(测角器的高度忽略不计.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin45°≈0.71,cos45°≈0.71)
大庄中学9年级学生在学习“解直角三角形”一章时,开展测量物体高度的实践活动,他们要测量校园内一棵大树的高度.如图,在大树前的平地上选一点A,测得由点A看大树顶端C的仰角为35°,在点A和大树之间选择一点B(A,B,D在同一直线上),测得由点B看大树顶端C的仰角为45°,再量得A,B两点间的距离为5.43米,求大树CD的高度(结果精确到0.1米).(测角器的高度忽略不计.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin45°≈0.71,cos45°≈0.71)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C′,则点B转过的路径长为$\frac{\sqrt{3}}{3}$π.
如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C′,则点B转过的路径长为$\frac{\sqrt{3}}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
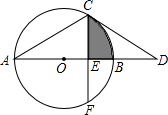 如图,AB为⊙O的直径,点C在⊙O上,过点C作CD交AB的延长线于点D,已知∠D=30°,弦CF⊥AB,垂足为E,且AC=2CE.
如图,AB为⊙O的直径,点C在⊙O上,过点C作CD交AB的延长线于点D,已知∠D=30°,弦CF⊥AB,垂足为E,且AC=2CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,总有$\frac{AB}{sinC}$=$\frac{AC}{sinB}$=$\frac{BC}{sinA}$,利用这个知识请解答下题:
在△ABC中,总有$\frac{AB}{sinC}$=$\frac{AC}{sinB}$=$\frac{BC}{sinA}$,利用这个知识请解答下题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com