
【题目】如图,![]() 是
是![]() 的弦,
的弦,![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 的直线交
的直线交![]() 的延长线于点
的延长线于点![]() .且
.且![]() .
.
(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)若![]() 的半径为
的半径为![]() ,
,![]() ,则
,则![]() 的长为 .
的长为 .
【答案】(1)详见解析;(2)2
【解析】
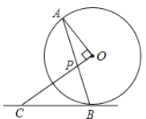
(1)由垂直定义得∠A+∠APO=90°,根据等腰三角形的性质由CP=CB得∠CBP=∠CPB,根据对顶角相等得∠CPB=∠APO,所以∠APO=∠CBP,而∠A=∠OBA,所以∠OBC=∠CBP+∠OBA=∠APO+∠A=90°,然后根据切线的判定定理得到BC是⊙O的切线;
(2)设BC=x,则PC=x,在Rt△OBC中,根据勾股定理得到(![]() )2+x2=(x+1)2,然后解方程即可.
)2+x2=(x+1)2,然后解方程即可.
(1)连结OB.

∵OP⊥OA,
∴∠A+∠APO=90°.
∵CP=CB,∴∠CBP=∠CPB.
∵∠CPB=∠APO,∴∠APO=∠CBP.
∵OA=OB,∴∠A=∠OBA.
∴∠OBC=∠CBP+∠OBA=∠APO+∠A=90°.
∴OB⊥BC.
∵点B在⊙O上,∴BC是⊙O的切线.
(2)解:设BC=x,则PC=x,
在Rt△OBC中,OB=![]() ,OC=CP+OP=x+1,
,OC=CP+OP=x+1,
∵OB2+BC2=OC2,
∴(![]() )2+x2=(x+1)2,
)2+x2=(x+1)2,
解得x=2,
即BC的长为2.


科目:初中数学 来源: 题型:
【题目】(操作发现)
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.

(1)请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;
(2)在(1)所画图形中,∠AB′B=____.
(问题解决)
(3)如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找PA,PB,PC三条线段之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找PA,PB,PC三条线段之间的数量关系.…
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形,如果所剪得的两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )

A.4:5B.2:5C.![]() :2D.
:2D.![]() :
:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
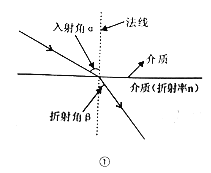
【题目】光线从空气射入水中会发生折射现象,发生折射时,满足的折射定律如图①所示:折射率![]() (
(![]() 代表入射角,
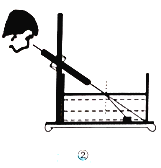
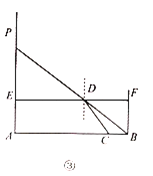
代表入射角,![]() 代表折射角).小明为了观察光线的折射现象,设计了图②所示的实验;通过细管可以看见水底的物块,但从细管穿过的直铁丝,却碰不上物块,图③是实验的示意图,点A,C,B在同一直线上,测得
代表折射角).小明为了观察光线的折射现象,设计了图②所示的实验;通过细管可以看见水底的物块,但从细管穿过的直铁丝,却碰不上物块,图③是实验的示意图,点A,C,B在同一直线上,测得![]() ,则光线从空射入水中的折射率n等于________.
,则光线从空射入水中的折射率n等于________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年春节,小娜家购买了4个灯笼,灯笼上分别写有“欢”、“度”、“春”、“节”(外观完全一样).
(1)小娜抽到“2019年”是 事件,“欢”字被抽中的是 事件;(填“不可能”或“必然”或“随机”).小娜从四个灯笼中任取一个,取到“春”的概率是 .
(2)小娜从四个灯笼中先后取出两个灯笼,请用列表法或画树状图法求小娜恰好取到“春”、“节”两个灯笼的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
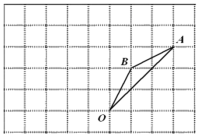
【题目】如图,在边长为1的正方形组成的网格中,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() ,
,![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,
,![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到
后得到![]() .
.
(1)画出![]() ,直接写出点
,直接写出点![]() ,
,![]() 的坐标;
的坐标;
(2)求在旋转过程中,点![]() 经过的路径的长;
经过的路径的长;
(3)求在旋转过程中,线段![]() 所扫过的面积.
所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )
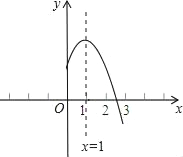
A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有3张相同的纸牌,它们分别标有数字3,﹣1,2,随机摸出一张纸牌不放回,记录其标有的数字为x,再随机摸取一张纸牌,记录其标有的数字为y,这样就确定点P的一个坐标为(x,y)
(1)用列表或画树状图的方法写出点P的所有可能坐标;
(2)写出点P落在双曲线![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
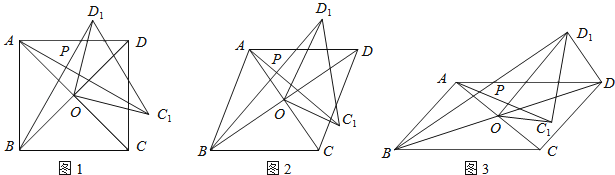
【题目】在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1,旋转角为θ(0°<θ<90°),连接AC1、BD1,AC1与BD1交于点P.
(1)如图1,若四边形ABCD是正方形.
①求证:△AOC1≌△BOD1.
②请直接写出AC1 与BD1的位置关系.
(2)如图2,若四边形ABCD是菱形,AC=5,BD=7,设AC1=kBD1.判断AC1与BD1的位置关系,说明理由,并求出k的值.
(3)如图3,若四边形ABCD是平行四边形,AC=5,BD=10,连接DD1,设AC1=kBD1.请直接写出k的值和AC12+(kDD1)2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com