
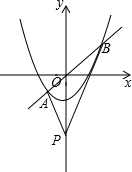
 ��ƽ��ֱ������ϵxOy�У�ֱ��y=kx��kΪ��������������y=$\frac{1}{3}$x2-2����A��B���㣬��A����y����࣬P������Ϊ��0��-4��������PA��PB��������˵����
��ƽ��ֱ������ϵxOy�У�ֱ��y=kx��kΪ��������������y=$\frac{1}{3}$x2-2����A��B���㣬��A����y����࣬P������Ϊ��0��-4��������PA��PB��������˵����| A�� | �� | B�� | �� | C�� | �� | D�� | �� |
���� ���ͼ1�����A����y��ĶԳƵ�ΪA�䣬�����ۢٳ����������֤����POA��ס�PBO���õ���AOP=��PBO������AOP�ǡ�PBO����ǣ���AOP����PBO���ɴ˲���ì�ܣ���˵���ٴ���
���ͼ2������ã�PA+AO����PB-BO��=16Ϊ��ֵ����˵���ڴ���
���������飬��õ�A��B���꣬�������BP��BO��BA����֤��ʽBP2=BO•BA��������˵���۴���
�ɸ���ϵ����ϵ�õ���S��PAB=2$\sqrt{9{k}^{2}+24}$����k=0ʱ��ȡ����СֵΪ4$\sqrt{6}$����˵������ȷ��
��� �⣺��A��m��km����B��n��kn��������m��0��n��0��
����y=$\frac{1}{3}$x2-2��y=kx�ã�$\frac{1}{3}$x2-2=kx����x2-3kx-6=0��
��m+n=3k��mn=-6��
��ֱ��PA�Ľ���ʽΪy=ax+b����P��0��-4����A��m��km������ã�
$\left\{\begin{array}{l}{b=-4}\\{ma+b=km}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=\frac{km+4}{m}}\\{b=-4}\end{array}\right.$��
��y=$\frac{km+4}{m}$x-4��
��y=0����x=$\frac{4m}{km+4}$��
��ֱ��PA��x��Ľ�������Ϊ��$\frac{4m}{km+4}$��0����
ͬ���ɵã�ֱ��PB�Ľ���ʽΪy=��$\frac{kn+4}{n}$��x-4��ֱ��PB��x�ύ������Ϊ��$\frac{4n}{kn+4}$��0����
��$\frac{4m}{km+4}$+$\frac{4n}{kn+4}$=$\frac{8kmn+16��n+n��}{��km+4����kn+4��}$=$\frac{8k����-6��+16��3k}{��km+4����kn+4��}$=0��
��ֱ��PA��PB��x��Ľ������y��Գƣ���ֱ��PA��PB����y��Գƣ�
��1��˵���ٴ����������£�
���ͼ1��ʾ����PA��PB����y��Գƣ�
���A����y��ĶԳƵ�A������PB�ϣ�
����OA�䣬��OA=OA�䣬��POA=��POA�䣮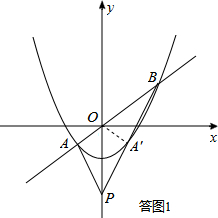
������ۣ�PO2=PA•PB��������PO2=PA��•PB��
��$\frac{PO}{PA��}$=$\frac{PB}{PO}$��
�֡ߡ�BPO=��BPO��
���POA��ס�PBO��
���POA��=��PBO��
���AOP=��PBO��
�ߡ�AOP�ǡ�PBO����ǣ�
���AOP����PBO��ì�ܣ�
��˵���ٴ���
˵���ڴ����������£�
��֪��$\frac{OB}{OA}$=-$\frac{n}{m}$��
��OB=-$\frac{n}{m}$OA��
�ɶԳƿ�֪��POΪ��APB�Ľ�ƽ���ߣ�
��$\frac{PB}{PA}$=$\frac{OB}{OA}$��
��PB=-$\frac{n}{m}$PA��
�ࣨPA+AO����PB-BO��=��PA+AO��[-$\frac{n}{m}$PA-��-$\frac{n}{m}$OA��]=-$\frac{n}{m}$��PA+AO����PA-OA��=-$\frac{n}{m}$��PA2-AO2����
���ͼ2��ʾ������A��AD��y���ڵ�D����OD=-km��PD=4+km��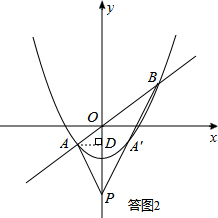
��PA2-AO2=��PD2+AD2��-��OD2+AD2��=PD2-OD2=��4+km��2-��-km��2=8km+16��
��m+n=3k����k=$\frac{1}{3}$��m+n����
��PA2-AO2=8•$\frac{1}{3}$��m+n��•m+16=$\frac{8}{3}$m2+$\frac{8}{3}$mn+16=$\frac{8}{3}$m2+$\frac{8}{3}$����-6��+16=$\frac{8}{3}$m2��
�ࣨPA+AO����PB-BO��=-$\frac{n}{m}$��PA2-AO2��=-$\frac{n}{m}$•$\frac{8}{3}$m2=-$\frac{8}{3}$mn=-$\frac{8}{3}$����-6��=16��
������PA+AO����PB-BO��Ϊ��ֵ������˵���ڴ���
˵���۴����������£�
��k=-$\frac{\sqrt{3}}{3}$ʱ�����������飺$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{3}}\\{y=\frac{1}{3}{x}^{2}-2}\end{array}\right.$����A��-2$\sqrt{3}$��2����B��$\sqrt{3}$��-1����
��BP2=12��BO•BA=2��6=12��
��BP2=BO•BA����˵���۴���
˵������ȷ���������£�
S��PAB=S��PAO+S��PBO=$\frac{1}{2}$OP•��-m��+$\frac{1}{2}$OP•n=$\frac{1}{2}$OP•��n-m��=2��n-m��=2$\sqrt{��m+n��^{2}-4mn}$=2$\sqrt{9{k}^{2}+24}$��
�൱k=0ʱ����PAB�������Сֵ����СֵΪ2$\sqrt{24}$=4$\sqrt{6}$��
��˵������ȷ��
������������ȷ��˵���ǣ��ܣ�
��ѡ��D��
���� �����Ǵ��������ۺ��⣬�ѶȺܴ�������ȵõ������������ۣ�����PA��PB�ĶԳ������ж�˵���ٵĻ������ݣ�����ϵ����ϵ�Ľ������ж�˵���ڡ��ܵĹؼ����ݣ���ȷ�������Ĺؼ��Ǵ����ѧ��������ƽʱ��ѧ֪ʶ�ڻ��ͨ��������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
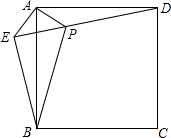 ��ͼ����������ABCD��ȡһ��E������AE��BE��DE������A��AE�Ĵ��߽�DE�ڵ�P����AE=AP=1��PB=2��
��ͼ����������ABCD��ȡһ��E������AE��BE��DE������A��AE�Ĵ��߽�DE�ڵ�P����AE=AP=1��PB=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | -2 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com