
分析 此题分情况考虑:当三角形的外心在三角形的内部时,根据勾股定理求得BD的长,再根据勾股定理求得AB的长;当三角形的外心在三角形的外部时,根据勾股定理求得BD的长,再根据勾股定理求得AB的长.
解答 解:如图1,当△ABC是锐角三角形时,连接AO并延长到BC于点D,
∵AB=AC,O为外心,
∴AD⊥BC,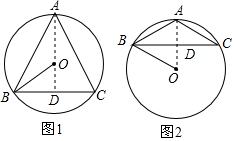
在Rt△BOD中,
∵OB=14,OD=6,
∴BD=$\sqrt{O{B}^{2}-O{D}^{2}}$=$\sqrt{1{4}^{2}-{6}^{2}}$=4$\sqrt{10}$.
在Rt△ABD中,根据勾股定理,得AB=$\sqrt{B{D}^{2}+A{D}^{2}}$=$\sqrt{(4\sqrt{10})^{2}+2{0}^{2}}$=4$\sqrt{35}$(cm);
如图2,当△ABC是钝角三角形时,连接AO交BC于点D,
同理得:BD=4$\sqrt{10}$.
∴AD=14-6=8,
在Rt△ABD中,根据勾股定理,得AB=$\sqrt{B{D}^{2}+A{D}^{2}}$=$\sqrt{{8}^{2}+(4\sqrt{10})^{2}}$=4$\sqrt{14}$(cm).
综上所述,AB的长是4$\sqrt{35}$cm或4$\sqrt{14}$cm.
点评 本题考查的是等腰三角形的性质、垂径定理和勾股定理,在解答此题时要注意进行分类讨论,不要漏解.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{m}^{2}+1}$ | B. | $\sqrt{\frac{a}{5}}$ | C. | $\sqrt{27}$ | D. | $\sqrt{5{a}^{2}b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 分数 | 100 | 90 | 80 | 70 | 60 | 50 |
| 人数 | 7 | 14 | 17 | 8 | 2 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “打开电视,正在播放新闻联播”是必然事件 | |
| B. | 某种彩票中奖概率为1%,是指买100张彩票一定有一张中奖 | |
| C. | 神舟飞船发射前需要对零部件进行抽样调查 | |
| D. | 了解某种节能灯的使用寿命适合抽样调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
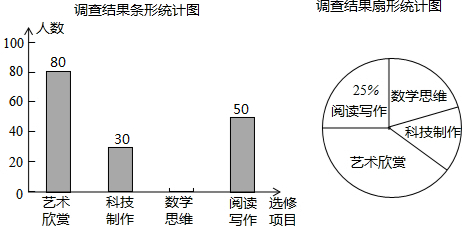
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com