
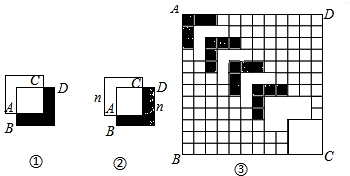
分析 【问题】(1)(2):图①②中,用原有一块正方形的面积减去一个重合的小正方形的面积即可求解,
【应用】:图③,(1)当n=2时,计算正方形的张数,可先云去掉最下面的一张,再来计算需要小正方形的纸片数,依次每向上一行需要一张纸片共10行,所以共用纸片10+1=11张;(2)当n=3时,计算方法相同,共用纸片数为9+1=10张;(3)当n=n时,共用的纸片数为12-n+1=13-n,即y=13-n;
【探究】归纳与总结,得到其中的规律.
解答 (1)根据题意,当n=2时,可得应盖住正方形有ABCD对角线上的12个格,
∴y=12-2+1=11,
(2)当n=3时,可得应盖住正方形有ABCD对角线上的13个格,
∴y=12-3+1=10,
故答案为:(1)11,(2)10
(3)当n=n时,可得应盖住正方形有ABCD对角线上的13个格,
∴y=12-n+1=13-n,
探究:第一个面积为n2,第二个面积为一个包边,共有12-n个,每个由2n-1个小正方形构成,包边的总面积为:(12-n)×(2n-1),
∴①S1=10×3+4=34,S2=144-34=110,
∴S1:S2=34:110=17:55.
②根据题意,得
${S}_{1}=(12-n)×(2n-1)+{n}^{2}$;
${S}_{2}=144-(12-n)×(2n-1)-{n}^{2}$,
若S1=S2时,
(12-n)×(2n-1)+n2=144-(12-n)×(2n-1)-n2,
解,得n=4或21.
∵2≤n≤11,
∴∴n=21舍去,
故n=4.
点评 本题是归纳与总结类题目,对于几何类题目根据图形的特征是解答问题的关键.


科目:初中数学 来源: 题型:填空题
 如图,点B、C把$\widehat{AD}$分成三等分,ED是⊙O的切线,过点B、C分别作半径的垂线段,已知∠E=45°,半径OD=1,则图中阴影部分的面积是$\frac{π}{8}$.
如图,点B、C把$\widehat{AD}$分成三等分,ED是⊙O的切线,过点B、C分别作半径的垂线段,已知∠E=45°,半径OD=1,则图中阴影部分的面积是$\frac{π}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小明回顾用尺规作一个角等于已知角的作图过程(如图所示),连接CD、C′D′得出了△OCD≌△O′C′D′,从而得到∠O=∠O′,其中小明作出△OCD≌△O′C′D′判定的依据是( )
小明回顾用尺规作一个角等于已知角的作图过程(如图所示),连接CD、C′D′得出了△OCD≌△O′C′D′,从而得到∠O=∠O′,其中小明作出△OCD≌△O′C′D′判定的依据是( )| A. | SSS | B. | SAS | C. | ASA | D. | AAS |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com