
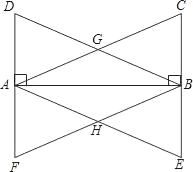
【题目】在Rt△ABC与Rt△ABD中,∠ABC=∠BAD=90°,AC=BD,AC,BD相交于点G,过点A作AE∥DB交CB的延长线于点E,过点B作BF∥CA交DA的延长线于点F,AE,BF相交于点H.
(1)证明:△ABD≌△BAC.
(2)四边形AHBG是什么样的四边形,请猜想并证明.
(3)若使四边形AHBG是正方形,还需在Rt△ABC添加一个什么条件?请添加条件并证明.
【答案】(1)见解析;(2) 四边形AHBG是菱形,理由见解析;(3) 需要添加的条件是AB=BC,理由见解析
【解析】
(1)可根据已知条件∠ABC=∠BAD=90°,AB=BA,AC=BD即可得到△ABC≌△BAD.
(2)由已知可得四边形AHBG是平行四边形,由(1)可知∠ABD=∠BAC,得到△GAB为等腰三角形,AHBG的两邻边相等,从而得到平行四边形AHBG是菱形.
(3)根据有一个角是直角的菱形是正方形,进行判断即可.
(1)∵∠ABC=∠BAD=90°,AB=BA,AC=BD,
∴Rt△ABC≌Rt△BAD(HL).
(2)四边形AHBG是菱形.
证明:∵AH∥GB,BH∥GA,
∴四边形AHBG是平行四边形.
∵△ABC≌△BAD,
∴∠ABD=∠BAC,
∴GA=GB,
∴平行四边形AHBG是菱形.
(3)需要添加的条件是AB=BC.
证明:∵AB=BC,∠ABC=90°,
∴△ABC是等腰直角三角形,
∴∠BAG=45°,
又∵△ABC≌△BAD,
∴∠ABG=∠BAG=45°,
∴∠AGB=90°,
∴菱形AHBG是正方形.


科目:初中数学 来源: 题型:
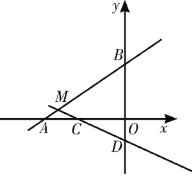
【题目】如图,在平面直角坐标系xOy中,已知直线AB:y=![]() x+4交x轴于点A,交y轴于点B.直线CD:y=-
x+4交x轴于点A,交y轴于点B.直线CD:y=-![]() x-1与直线AB相交于点M,交x轴于点C,交y轴于点D.
x-1与直线AB相交于点M,交x轴于点C,交y轴于点D.
(1)直接写出点B和点D的坐标.
(2)若点P是射线MD的一个动点,设点P的横坐标是x,△PBM的面积是S,求S与x之间的函数关系,并指出x的取值范围.
(3)当S=10时,平面直角坐标系内是否存在点E,使以点B,E,P,M为顶点的四边形是平行四边形?若存在,共有几个这样的点?请求出其中一个点的坐标(写出求解过程);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别用火柴棍连续搭建等边三角形和正六边形,公共边只用一根火柴棍.如果搭建等边三角形和正六边形共用了![]() 根火柴,并且等边三角形的个数比正六边形的个数多
根火柴,并且等边三角形的个数比正六边形的个数多![]() ,那么连续搭建的等边三角形的个数是( )
,那么连续搭建的等边三角形的个数是( )
![]() ……
…… ……
……
A.![]() B.
B.![]() C.
C.![]() D.以上答案都不对
D.以上答案都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是 ;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点F,则CF的长为
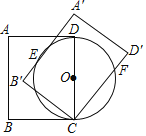
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行知识大赛,![]() 校、
校、![]() 校各派出
校各派出![]() 名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
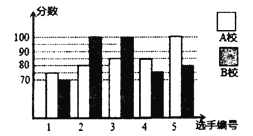
(1)根据图示填写下表:
平均数 | 中位数 | 众数 | |
|
| ||
|
| 80 |
(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b)
(1)求b,m的值
(2)垂直于x轴的直线x=a与直线l1,l2分别相交于C,D,若线段CD长为2,求a的值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接“炎帝故里寻根节”,某校开展了主题为“炎帝文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”“比较了解”“基本了解”“不太了解”四个等级,整理调查数据制成了下面的表格和如图所示的不完整的扇形统计图.
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 50 | m | 40 | 20 |

根据以上提供的信息,解答下列问题:
(1)本次问卷调查共抽取的学生人数为________,表中m的值为________;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生1 500人,请根据调查结果估计这些学生中“不太了解”炎帝文化知识的人数约为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com