
【题目】如图1,在平面直径坐标系中,抛物线y=ax2+bx﹣2与x轴交于点A(﹣3,0).B(1,0),与y轴交于点C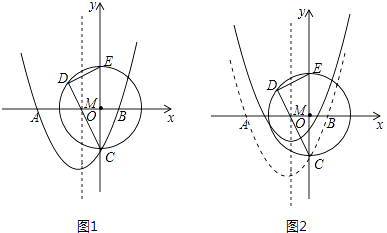
(1)直接写出抛物线的函数解析式;
(2)以OC为半径的⊙O与y轴的正半轴交于点E,若弦CD过AB的中点M,试求出DC的长;
(3)将抛物线向上平移 ![]() 个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值.
个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值.
【答案】
(1)
解:将点A(﹣3,0)、B(1,0)代入y=ax2+bx﹣2中,
得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线的函数解析式为y= ![]() x2+
x2+ ![]() x﹣2
x﹣2
(2)
解:令y= ![]() x2+
x2+ ![]() x﹣2中x=0,则y=﹣2,
x﹣2中x=0,则y=﹣2,
∴C(0,﹣2),
∴OC=2,CE=4.
∵A(﹣3,0),B(1,0),点M为线段AB的中点,
∴M(﹣1,0),
∴CM= ![]() =
= ![]() .
.
∵CE为⊙O的直径,
∴∠CDE=90°,
∴△COM∽△CDE,
∴ ![]() ,
,
∴DC= ![]() .
.
(3)
解:将抛物线向上平移 ![]() 个单位长度后的解析式为y=
个单位长度后的解析式为y= ![]() x2+
x2+ ![]() x﹣2+
x﹣2+ ![]() =
= ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() ,
,
令y= ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() 中y=0,即
中y=0,即 ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() =0,
=0,
解得:x1= ![]() ,x2=
,x2= ![]() .
.
∵点P在第三象限,
∴ ![]() <x<0.
<x<0.
过点P作PP′⊥y轴于点P′,过点D作DD′⊥y轴于点D′,如图所示.
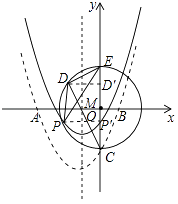
(方法一):在Rt△CDE中,CD= ![]() ,CE=4,
,CE=4,
∴DE= ![]() =
= ![]() ,sin∠DCE=
,sin∠DCE= ![]() =
= ![]() ,
,
在Rt△CDD′中,CD= ![]() ,∠CD′D=90°,
,∠CD′D=90°,
∴DD′=CDsin∠DCE= ![]() ,CD′=
,CD′= ![]() =
= ![]() ,
,
∴OD′=CD′﹣OC= ![]() ,
,
∴D(﹣ ![]() ,
, ![]() ),D′(0,
),D′(0, ![]() ).
).
∵P(x, ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() ),
),
∴P′(0, ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() ).
).
∴S△PDE=S△DD′E+S梯形DD′P′P﹣S△EPP′= ![]() DD′ED′+
DD′ED′+ ![]() (DD′+PP′)D′P′﹣
(DD′+PP′)D′P′﹣ ![]() PP′EP′=﹣
PP′EP′=﹣ ![]() ﹣
﹣ ![]() x+2(
x+2( ![]() <x<0),
<x<0),
∵S△PDE=﹣ ![]() ﹣
﹣ ![]() x+2=﹣
x+2=﹣ ![]() +
+ ![]() ,
, ![]() <﹣
<﹣ ![]() <0,
<0,
∴当x=﹣ ![]() 时,S△PDE取最大值,最大值为
时,S△PDE取最大值,最大值为 ![]() .
.
故:△PDE的面积关于x的函数关系式为S△PDE=﹣ ![]() ﹣
﹣ ![]() x+2(
x+2( ![]() <x<0),且△PDE面积的最大值为
<x<0),且△PDE面积的最大值为 ![]() .
.
(方法二):在Rt△CDE中,CD= ![]() ,CE=4,
,CE=4,
∴DE= ![]() =
= ![]() ,
,
∵∠CDE=∠CD′D=90°,∠DCE=∠D′CD,
∴△CDE∽△CD′D,
∴ ![]() =
= ![]() ,
,
∴DD′= ![]() ,CD′=
,CD′= ![]() ,
,
∴∴OD′=CD′﹣OC= ![]() ,
,
∴D(﹣ ![]() ,
, ![]() ),D′(0,
),D′(0, ![]() ).
).
∵P(x, ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() ),
),
∴P′(0, ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() ).
).
∴S△PDE=S△DD′E+S梯形DD′P′P﹣S△EPP′= ![]() DD′ED′+
DD′ED′+ ![]() (DD′+PP′)D′P′﹣
(DD′+PP′)D′P′﹣ ![]() PP′EP′=﹣
PP′EP′=﹣ ![]() ﹣
﹣ ![]() x+2(
x+2( ![]() <x<0),
<x<0),
∵S△PDE=﹣ ![]() ﹣
﹣ ![]() x+2=﹣
x+2=﹣ ![]() +
+ ![]() ,
, ![]() <﹣
<﹣ ![]() <0,
<0,
∴当x=﹣ ![]() 时,S△PDE取最大值,最大值为
时,S△PDE取最大值,最大值为 ![]() .
.
故:△PDE的面积关于x的函数关系式为S△PDE=﹣ ![]() ﹣
﹣ ![]() x+2(
x+2( ![]() <x<0),且△PDE面积的最大值为
<x<0),且△PDE面积的最大值为 ![]() .
.
【解析】(1)由点A、B的坐标利用待定系数法即可求出抛物线的解析式;(2)令抛物线解析式中x=0求出点C的坐标,根据点A、B的坐标即可求出其中点M的坐标,由此即可得出CM的长,根据圆中直径对的圆周角为90°即可得出△COM∽△CDE,根据相似三角形的性质即可得出 ![]() ,代入数据即可求出DC的长度;(3)根据平移的性质求出平移后的抛物线的解析式,令其y=0,求出平移后的抛物线与x轴的交点坐标,由此即可得出点P横坐标的范围,再过点P作PP′⊥y轴于点P′,过点D作DD′⊥y轴于点D′,通过分割图形求面积法找出S△PDE关于x的函数关系式,利用配方结合而成函数的性质即可得出△PDE面积的最大值.
,代入数据即可求出DC的长度;(3)根据平移的性质求出平移后的抛物线的解析式,令其y=0,求出平移后的抛物线与x轴的交点坐标,由此即可得出点P横坐标的范围,再过点P作PP′⊥y轴于点P′,过点D作DD′⊥y轴于点D′,通过分割图形求面积法找出S△PDE关于x的函数关系式,利用配方结合而成函数的性质即可得出△PDE面积的最大值.
【考点精析】利用二次函数的性质对题目进行判断即可得到答案,需要熟知增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )

A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用为0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级进行了模拟考试后,张老师对九(2)班全体同学“满分值为6分得一道解答题的得分”情况进行了统计,绘制成下表(学生得分均为整数分):

由于在填表时不慎把墨水滴在表格上,致使表中数据不完整,但已知全班同学此题的平均得分为4分,结合上表回答下列问题:
(1)九(2)班学生共有多少人?
(2)若本年级学生共有540人,请你用此样本估计整个年级有多少同学此题得满分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成证明并写出推理根据:
已知,如图,∠1=132°,∠ACB=48°,∠2=∠3.
求证:∠CDB=∠FHB.
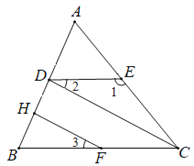
证明:
∵∠1=132°,∠ACB=48° (已知)
∴∠1+∠ACB=180°
∴DE∥BC ( )
∴∠2=∠ ( )
又∵∠2=∠3 (已知)
∴∠3=∠ (等量代换)
∴HF∥DC ( )
∴∠CDB=∠FHB ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心O出发,按图中箭头所示的方向,依次爬完下列三条线路:(1)线段OA、(2)半圆弧AB、(3)线段BO后,回到出发点。已知蚂蚁在爬行过程中保持匀速,且在寻找到食物后停下来吃了2分钟。蚂蚁离出发点的距离s(蚂蚁所在位置与O点之间线段的长度)与时间t之间的图象如图2所示,问:
(1)花坛的半径是_______米,蚂蚁是在上述三条线路中的哪条上寻找到了食物_________(填(1)、(2)、或(3));
(2)蚂蚁的速度是_______米/分钟;

(3)蚂蚁从O点出发,直到回到O点,一共用时多少分钟?(![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
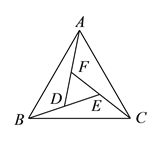
【题目】如图 ,在正![]() 的内部,作
的内部,作![]() ,
, ![]() ,
, ![]() ,
, ![]() 两两相交于
两两相交于![]() ,
, ![]() ,
, ![]() 三点 (
三点 (![]() ,
, ![]() ,
, ![]() 三点不重合).
三点不重合).
(![]() )
)![]() ,
, ![]() ,
, ![]() 是否全等?如果是,请选择其中一对进行证明.
是否全等?如果是,请选择其中一对进行证明.
(![]() )
)![]() 是否为正三角形?请说明理由.
是否为正三角形?请说明理由.
(![]() )进一步探究发现,
)进一步探究发现, ![]() 的三边存在一定的等量关系,设
的三边存在一定的等量关系,设![]() ,
, ![]() ,
, ![]() ,请探索
,请探索![]() ,
, ![]() ,
, ![]() 满足的等量关系.
满足的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=x2+bx+c与y=x的图像如图所示,有以下结论:
①b2﹣4c>0;②3b+c+6=0;③当1<x<3时,x2+(b﹣1)x+c<0;
④ ![]() ,其中正确的有
,其中正确的有
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com