
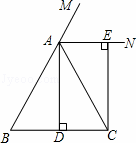
已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
科目:初中数学 来源: 题型:
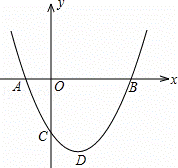
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1,3.与y轴负半轴交于点C,在下面五个结论中:
①2a﹣b=0;②a+b+c>0;③c=﹣3a;④只有当a=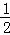 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a值可以有四个.
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a值可以有四个.
其中正确的结论是 .(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
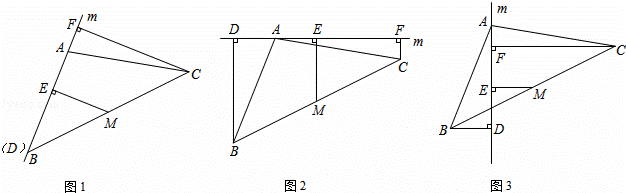
已知△ABC中,M为BC的中点,直线m绕点A旋转,过B、M、C分别作BD⊥m于D,ME⊥m于E,CF⊥m于F.
(1)当直线m经过B点时,如图1,易证EM=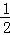 CF.(不需证明)
CF.(不需证明)
(2)当直线m不经过B点,旋转到如图2、图3的位置时,线段BD、ME、CF之间有怎样的数量关系?请直接写出你的猜想,并选择一种情况加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
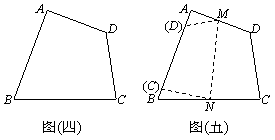
图(四)为某四边形ABCD纸片,其中ÐB=70°,ÐC=80°。若将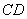 迭合在
迭合在 上,出现折线
上,出现折线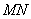 ,再将纸片展开后,M、N 两点分别在
,再将纸片展开后,M、N 两点分别在 、
、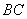 上,如图(五)所示,则ÐMNB的度数为何?
上,如图(五)所示,则ÐMNB的度数为何?
(A) 90 (B) 95 (C) 100 (D) 105
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com