
 如图,△ABC中,AC=BC,∠ACB=Rt∠,点P是线段BC延长线上任意一点,以AP为直角边作等腰直角△APD,且∠APD=Rt∠,连结BD
如图,△ABC中,AC=BC,∠ACB=Rt∠,点P是线段BC延长线上任意一点,以AP为直角边作等腰直角△APD,且∠APD=Rt∠,连结BD分析 (1)设AD与PB交于点K.由△AKB∽△PKD,推出△AKP∽△BKD,推出∠ADB=∠APK,∠PAK=∠DBK=45°,推出∠ABD=∠∠DBK=90°,推出∠ABD=∠ACP,由∠ADB=∠APC,推出△ABD∽△ACP,即可解决问题.
(2)结论:∠PBD的度数是定值,∠PBD=45°.由(1)可知△AKP∽△BKD,即可推出PAK=∠DBK=45°.
(3)①在Rt△ABC中,由AB=$\sqrt{2}$,推出BC=AC=1,在Rt△ACP中,PA=$\sqrt{A{C}^{2}+P{C}^{2}}$=$\sqrt{1+{x}^{2}}$,由△ABD∽△ACP,推出$\frac{AC}{AB}$=$\frac{PC}{BD}$,推出$\frac{1}{\sqrt{2}}$=$\frac{x}{BD}$,可得BD=$\sqrt{2}$x,
根据S=S△ABD+S△APD-S△ABP计算即可.②取AD的中点O,连接OB、OP.由∠ABD=∠APD=90°,推出OB=OA=OP=OD,推出点O是△PBD的外接圆的圆心,求出线段AD即可解决问题.
解答 (1)证明:如图,设AD与PB交于点K.
∵CA=BC,∠ACB=90°,
∴∠ABC=45°,
∵PA=PD,∠APD=90°,
∴∠PDK=∠PAD=∠ABK=45°,∵∠AKB=∠DKP,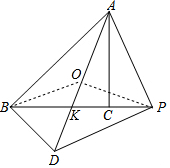
∴△AKB∽△PKD,
∴$\frac{AK}{PK}$=$\frac{BK}{DK}$,
∴$\frac{AK}{KB}$=$\frac{PK}{DK}$,∵∠AKP=∠BKD,
∴△AKP∽△BKD,
∴∠ADB=∠APK,∠PAK=∠DBK=45°,
∴∠ABD=∠∠DBK=90°,
∴∠ABD=∠ACP,∵∠ADB=∠APC,
∴△ABD∽△ACP,
∴$\frac{AC}{AP}$=$\frac{AB}{AD}$;
(2)解:结论:∠PBD的度数是定值,∠PBD=45°.
理由:由(1)可知△AKP∽△BKD,
∴PAK=∠DBK=45°,
∴在点P运动过程中,∠PBD的度数是定值,∠PBD=45°
(3)解:①在Rt△ABC中,∵AB=$\sqrt{2}$,
∴BC=AC=1,
在Rt△ACP中,PA=$\sqrt{A{C}^{2}+P{C}^{2}}$=$\sqrt{1+{x}^{2}}$,
∵△ABD∽△ACP,
∴$\frac{AC}{AB}$=$\frac{PC}{BD}$,
∴$\frac{1}{\sqrt{2}}$=$\frac{x}{BD}$,
∴BD=$\sqrt{2}$x,
∴S=S△ABD+S△APD-S△ABP=$\frac{1}{2}$•$\sqrt{2}$•$\sqrt{2}$x-$\frac{1}{2}$•$\sqrt{1+{x}^{2}}$•$\sqrt{1+{x}^{2}}$-$\frac{1}{2}$(1+x)•1=$\frac{1}{2}$x2+$\frac{1}{2}$x.
②取AD的中点O,连接OB、OP.
∵∠ABD=∠APD=90°,
∴OB=OA=OP=OD,
∴点O是△PBD的外接圆的圆心,
∵S=$\frac{3}{8}$,
∴$\frac{1}{2}$x2+$\frac{1}{2}$x=$\frac{3}{8}$,
解得x=$\frac{1}{2}$或-$\frac{3}{2}$(舍弃),
∴PC=$\frac{1}{2}$,
由(2)可知BD=$\sqrt{2}$x,
∴BD=$\frac{\sqrt{2}}{2}$,
在Rt△ABD中,AD=$\sqrt{A{B}^{2}+B{D}^{2}}$=$\sqrt{(\sqrt{2})^{2}+(\frac{\sqrt{2}}{2})^{2}}$=$\frac{\sqrt{10}}{2}$,
∴OD=$\frac{1}{2}$AD=$\frac{\sqrt{10}}{4}$,
∴△PBD的外接圆的半径为$\frac{\sqrt{10}}{4}$.
点评 本题考查圆综合题、相似三角形的判定和性质、勾股定理、三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,学会用分割法求三角形面积,学会其中外接圆的圆心的方法,属于中考压轴题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案科目:初中数学 来源: 题型:解答题
| 摸球总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
| “和为8“出现的频数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
| “和为8“出现的频率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,射线AB∥射线CD,∠CAB与∠ACD的平分线交于点E,AC=4,点P是射线AB上的一动点,连结PE并延长交射线CD于点Q.给出下列结论:①△ACE是直角三角形;②S四边形APQC=2S△ACE;③设AP=x,CQ=y,则y关于x的函数表达式是y=-x+4(0≤x≤4),其中正确的是( )
如图,射线AB∥射线CD,∠CAB与∠ACD的平分线交于点E,AC=4,点P是射线AB上的一动点,连结PE并延长交射线CD于点Q.给出下列结论:①△ACE是直角三角形;②S四边形APQC=2S△ACE;③设AP=x,CQ=y,则y关于x的函数表达式是y=-x+4(0≤x≤4),其中正确的是( )| A. | ①②③ | B. | ①② | C. | ①③ | D. | ②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{15}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com