
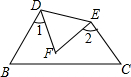
 如图,将纸片△ABC沿DE折叠,点A落在点F处.
如图,将纸片△ABC沿DE折叠,点A落在点F处.分析 (1)由折叠的性质得出∠ADE=∠EDF,∠AED=∠DEF,得出∠1+∠2+2(∠ADE+∠AED)=360°,由已知条件得出∠ADE+∠AED=140°,即可得出∠A的度数;
(2)由折叠的性质和平角的定义得出∠1+2∠ADE+∠2+2∠AED=360°①,由三角形内角和定理得出2(∠A+∠ADE+∠AED)=360°②,由①②即可得出∠1+∠2=2∠A.
解答 解:(1)如图所示: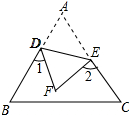 ∵将纸片△ABC沿DE折叠,点A落在点F处,
∵将纸片△ABC沿DE折叠,点A落在点F处,
∴∠ADE=∠EDF,∠AED=∠DEF,
∴∠1+2∠ADE+∠2+2∠AED=180°+180°,
∴∠1+∠2+2(∠ADE+∠AED)=360°,
又∵∠1+∠2=80°,
∴∠ADE+∠AED=140°,
∴∠A=180°-(∠ADE+∠AED)=40°.
(2)∠1+∠2=2∠A,理由如下:
由折叠的性质得:∠1+2∠ADE=180°,∠2+2∠AED=180°,
∴∠1+2∠ADE+∠2+2∠AED=360°①,
又∵∠A+∠ADE+∠AED=180°,
∴2(∠A+∠ADE+∠AED)=360°②,
由①②得:∠1+∠2=2∠A.
点评 本题考查了三角形内角和定理、折叠的性质;熟练掌握三角形内角和定理,并能进行推理计算是解决问题的关键.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:解答题
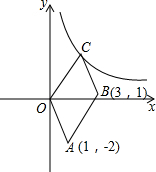 如图,在平面直角坐标系中,四边形OABC是平行四边形,O(0,0),A(1,-2),B(3,1),反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点C.
如图,在平面直角坐标系中,四边形OABC是平行四边形,O(0,0),A(1,-2),B(3,1),反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
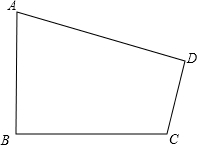 威海刘公岛是全国知名的旅游景区之一,该岛的近似形状如图所示.经地质人员测量得知:AB=4km,CD=2km,∠A=60°,∠B=∠D=90°.利用这些条件你能求出该岛的面积吗?
威海刘公岛是全国知名的旅游景区之一,该岛的近似形状如图所示.经地质人员测量得知:AB=4km,CD=2km,∠A=60°,∠B=∠D=90°.利用这些条件你能求出该岛的面积吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com