练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
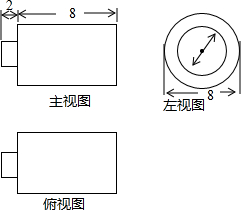
    19．如图，是某几何体的三视图，根据图中所标的数据求得该几何体的体积为（　　）
    A．120πB．132πC．136πD．236π

    分析 根据给出的几何体的三视图可知几何体是由大小两个圆柱组成，从而根据三视图的特点得知高和底面直径，代入体积公式计算即可．

    解答 解：由三视图可知，几何体是由大小两个圆柱组成，
    故该几何体的体积为：π×22×2+π×42×8
    =8π+128π
    =136π．
    故选：C．

    点评 本题考查的是由三视图判断几何体的形状并计算几何体的体积，由该三视图中的数据确定圆柱的底面直径和高是解本题的关键，本题体现了数形结合的数学思想．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    9．由若干个相同的小正方体搭成一个几何体，从上面看，它的形状图如图所示，小正方形中的数字表示该位置上的小正方体的个数，则从左面看这个几何体的形状是（　　）
    A．B．C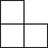．D．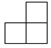

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

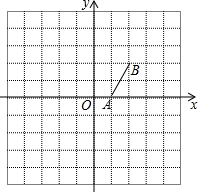    10．如图，在正方形网格中，每个小正方形的边长为1个单位长度．平面直角坐标系xOy的原点O在格点上，x轴、y轴都在网格线上，线段A、B在格点上．
    （1）将线段AB绕点O逆时针旋转90°得到线段A1B1，试在图中画出线段A1B1．
    （2）在（1）的条件下，线段A2B2与线段A1B1关于原点O成中心对称，请在图中画出线段A2B2．
    （3）在（1）、（2）的条件下，点P是此平面直角坐标系内的一点，当以点A、B、B2、P为顶点的四边形为平行四边形时，请你直接写出点P的坐标：（1，-4）、（3，0）、（1，4）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列分式运算，正确的是（　　）
    A．（$\frac{3x}{5y}$）2=$\frac{3{x}^{2}}{5{y}^{2}}$B．$\frac{1}{x-y}-\frac{1}{y-x}$=0C．$\frac{1}{3x}+\frac{1}{3y}=\frac{1}{3（x+y）}$D．（$\frac{{x}^{2}}{-y}$）3=-$\frac{{x}^{6}}{{y}^{3}}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，抛物线y=ax2+bx-4与x轴交于点A（-2，0）、B（4，0），与y轴交于点C，过点C作x轴的平行线交抛物线于点D，连接AC，作直线BC．
    （1）求抛物线y=ax2+bx-4的表达式；
    （2）如图2，点E（x，0）是线段OB上的一点，过点E作与x轴垂直的直线与直线BC交于点F，与抛物线交于点G．
    ①线段FG的长是否存在最大值？若存在，求出这个最大值；若不存在，说明理由；
    ②连接CG，当∠DCG=∠ACO时，求点G的坐；
    （3）若点P是直线BC下方的抛物线上的一点，点Q在y轴上，点M在线段BC上，当以C，P，Q，M为顶点的四边形是菱形时，直接写出菱形的边长．

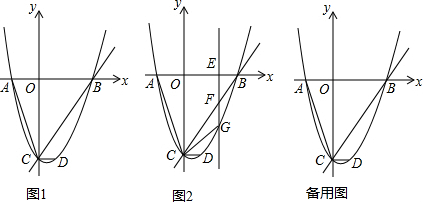
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图1，二次函数y=$\frac{3}{4}$x2+bx+c与一次函数y=$\frac{3}{4}$x-3的图象都经过x轴上点A（4，0）和y轴上点B（0，-3），过动点M（m，0）（0＜m＜4）作x轴的垂线交直线AB于点C，交抛物线于点P．
    （1）求b，c的值；
    （2）点M在运动的过程中，能否使△PBC为直角三角形？如果能，求出点P的坐标；如果不能，请说明理由；
    （3）如图2，过点P作PD⊥AB于点，设△PCD的面积为S1，△ACM的面积为2，若$\frac{{S}_{1}}{{S}_{2}}$=$\frac{36}{25}$，
    ①求m的值；
    ②如图3，将线段OM绕点O顺时针旋转得到OM′，旋转角为α（0°＜α＜90°），连接M'A、M'B，求M'A+$\frac{2}{3}$M'B的最小值．

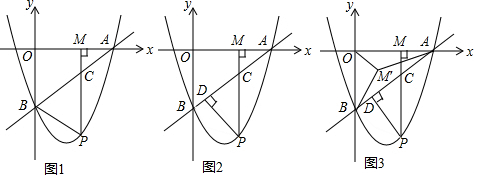
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

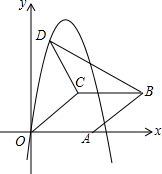    11．如图，在平面直角坐标系中，菱形OABC的顶点A在x轴正半轴上，顶点C的坐标为（4，3），D是抛物线y=-（x-3）2+9上一点，且在x轴上方，则△BCD面积的最大值为15．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．（1）计算：（-1）2017+|$\sqrt{3}$-3|+（tan30°）-1
    （2）解方程组：$\left\{\begin{array}{l}{x-y=5}\\{2x+y=4}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

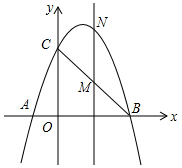    9．如图，二次函数y=ax2-2ax+3（a≠0）的图象与x、y轴交于A、B、C三点，
    其中AB=4，连接BC．
    （1）求二次函数的对称轴和函数表达式；
    （2）若点M是线段BC上的动点，设点M的横坐标为m，过点M作MN∥y轴交抛物线于点N，求线段MN的最大值；
    （3）当0≤x≤t时，则3≤y≤4，直接写出t的取值范围．

    查看答案和解析>>

    同步练习册答案