
 x+2的图象与x轴、y轴分别交于A、B,以AB为边在第二象限内作等边△ABC.
x+2的图象与x轴、y轴分别交于A、B,以AB为边在第二象限内作等边△ABC.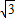 ,0),(0,2),OA=2
,0),(0,2),OA=2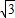 ,OB=2,因此∠OAB=30°,因为三角形CAB是个等边三角形,因此∠CAB=60°,那么CA⊥OA,C点的横坐标就是A点的横坐标,如果求出CA的长那么就能求出C点的坐标了,根据AC=AB,有OA、OB的长,根据勾股定理我们可求出AB的长,也就求出AC的长,那么C点的坐标就求出来了.
,OB=2,因此∠OAB=30°,因为三角形CAB是个等边三角形,因此∠CAB=60°,那么CA⊥OA,C点的横坐标就是A点的横坐标,如果求出CA的长那么就能求出C点的坐标了,根据AC=AB,有OA、OB的长,根据勾股定理我们可求出AB的长,也就求出AC的长,那么C点的坐标就求出来了.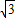 ,
,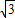 -1,那么P的横坐标就是1-
-1,那么P的横坐标就是1-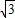 ,代入函数式中即可求出P的坐标为(1-
,代入函数式中即可求出P的坐标为(1-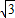 ,
,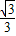 +1)
+1)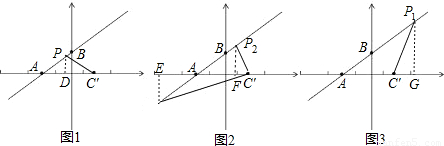
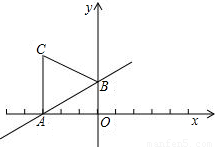 解:(1)根据直线的函数关系式,我们可得出A点的坐标为(-2
解:(1)根据直线的函数关系式,我们可得出A点的坐标为(-2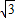 ,0),B点的坐标为(0,2),
,0),B点的坐标为(0,2),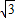 ,OB=2,直角三角形ABO中,AG=
,OB=2,直角三角形ABO中,AG=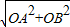 =4,∠BAO=30°,
=4,∠BAO=30°, ,4).
,4).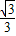 x+b,
x+b,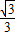 x+6,
x+6, m+6=1,m=-5
m+6=1,m=-5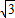 ,
,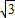 ,1),
,1),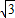 ,
,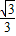 +1),
+1),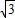 ,-
,-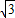 -1)或(3-
-1)或(3-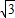 ,
,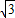 +1),
+1),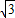 +3,3+3
+3,3+3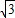 ),
), ,
,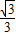 +1)或(-3-
+1)或(-3-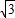 ,-
,-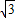 -1)或(3-
-1)或(3-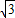 ,
,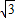 +1)或(
+1)或(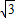 +3,3+3
+3,3+3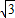 ).
).

科目:初中数学 来源:2009年四川省攀枝花市东区中考数学二模试卷(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2009年四川省攀枝花市东区中考数学二模试卷(解析版) 题型:选择题
 (2009•攀枝花二模)如图是二次函数y=ax2+bx+c的图象,下列结论中:①abc>0;②b=2a;③a+b+c<0;④a-b+c>0;⑤4a+2b+c<0.正确的个数是( )
(2009•攀枝花二模)如图是二次函数y=ax2+bx+c的图象,下列结论中:①abc>0;②b=2a;③a+b+c<0;④a-b+c>0;⑤4a+2b+c<0.正确的个数是( )查看答案和解析>>
科目:初中数学 来源:2009年四川省攀枝花市东区中考数学二模试卷(解析版) 题型:选择题




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com