
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据二次根据的运算,分别验证五个等式的正误,由此即可得出结论.
解答 解:①$\sqrt{20}$=2$\sqrt{5}$,故①不正确;
②$\sqrt{16\frac{1}{4}}$=$\sqrt{\frac{65}{4}}$=$\frac{\sqrt{13}}{2}$,故②不正确;
③$\sqrt{8}$-$\sqrt{2}$=2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$,故③正确;
④$\sqrt{(-2)^{2}}$=$\sqrt{4}$=2,故④不正确;
⑤$\frac{\sqrt{27}-\sqrt{12}}{3}$=$\frac{3\sqrt{3}-2\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$,故⑤不正确.
综上所述:正确的结论为③.
故选A.
点评 本题考查了二次根式的加减法以及二次根式的性质与化简,熟练掌握二次根式化简的方法是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 第1个 | B. | 第2个 | C. | 第3个 | D. | 第4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
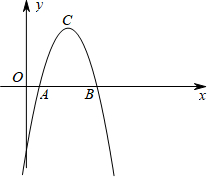 如图,已知与x轴交于点A(1,0)和B(5,0)的抛物线l的顶点为C(3,4),抛物线l′和l关于x轴对称.
如图,已知与x轴交于点A(1,0)和B(5,0)的抛物线l的顶点为C(3,4),抛物线l′和l关于x轴对称.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com