
【题目】如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20m,高度DC=30m则信号发射塔顶端到地面的高度(即FG的长)为( )
A.(35 ![]() +55)m
+55)m
B.(25 ![]() +45)m
+45)m
C.(25 ![]() +75)m
+75)m
D.(50+20 ![]() )m
)m
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某服装厂生产一批男衬衫,经过抽样调查60名中年男子,得知所需衬衫型号的人数如表所示.求出它的中位数是74,众数是76,平均数是74.6,下列说法正确的是( )

A. 所需78号人数太少,78号的可以不生产
B. 这批衬衫可以一律按身长是74.6这个平均数生产
C. 因为众数是76,故76号的生产量要占第一位
D. 因为中位数是74,故74号的生产量要占第一位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识生成)
我们已经知道,通过不同的方法表示同一图形的面积,可以探求相应的等式.
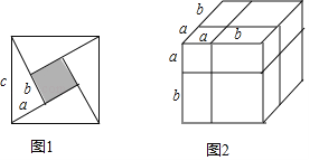
2002年8月在北京召开了国际数学大会,大会会标如图1所示,它是由四个形状大小完全相同的直角三角形与中间的小正方形拼成的一个大正方形,直角三角形的两条直角边长分别为a、b ( a<b ),斜边长为c.
(1)图中阴影部分的面积用两种方法可分别表示为 、 ;
(2)你能得出的a,b,c之间的数量关系是 (等号两边需化为最简形式);
(3)一直角三角形的两条直角边长为6和8,则其斜边长为 .
(知识迁移)
通过不同的方法表示同一几何体的体积,也可以探求相应的等式.如图2是边长为a+b的正方体,被如图所示的分割线分成8块.
(4)用不同方法计算这个正方体体积,就可以得到一个等式,这个等式可以为 .(等号两边需化为最简形式)
(5)已知a+b=3,ab=1,利用上面的规律求a3+b3的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面内,线段AB=6,P为线段AB上的动点,三角形纸片CDE的边CD所在的直线与线段AB垂直相交于点P,且满足PC=PA.若点P沿AB方向从点A运动到点B,则点E运动的路径长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
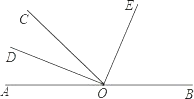
【题目】如图,O为直线AB上一点,∠AOC=50°20′,OD平分∠AOC,∠DOE=90°.
(1)求∠DOB的度数;
(2)请你通过计算说明OE是否平分∠COB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)( )
A.164m
B.178m
C.200m
D.1618m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB>∠ABC.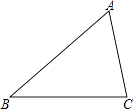
(1)用直尺和圆规在∠ACB的内部作射线CM,使∠ACM=∠ABC(不要求写作法,保留作图痕迹);
(2)若(1)中的射线CM交AB于点D,AB=9,AC=6,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)2020年9月的日历如图1所示,用1×3的长方形框出3个数.如果任意圈出一横行左右相邻的三个数,设最小的数为x,用含x的式子表示这三个数的和为 ;如果任意圈出一竖列上下相邻的三个数,设最小的数为y,用含y的式子表示这三个数的和为
(2)如图2,用一个2×2的正方形框出4个数,是否存在被框住的4个数的和为96?如果存在,请求出这四个数中的最小的数字;如果不存在,请说明理由
(3)如图2,用一个3×3的正方形框出9个数,在框出的9个数中,记前两行共6个数的和为a1,最后一行3个数的和为a2.若|a1﹣a2|=6,请求出正方形框中位于最中心的数字m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com