
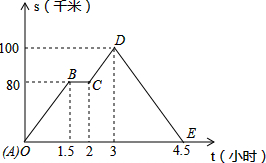
 如图,图象(折线ABCDE)描述了一汽车在某一直路上的行驶 过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的变量关系,根据图中提供的信息,填空:
如图,图象(折线ABCDE)描述了一汽车在某一直路上的行驶 过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的变量关系,根据图中提供的信息,填空:科目:初中数学 来源: 题型:
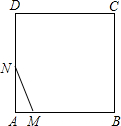 如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自A点出发沿折线AD-DC-CB以每秒3cm的速度运动,到达B点时运动同时停止.设△AMN的面积为y(cm2).运动时间为x(秒),则下列图象中能大致反映y与x之间函数关系的是( )
如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自A点出发沿折线AD-DC-CB以每秒3cm的速度运动,到达B点时运动同时停止.设△AMN的面积为y(cm2).运动时间为x(秒),则下列图象中能大致反映y与x之间函数关系的是( )A、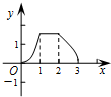 | B、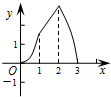 | C、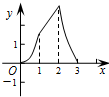 | D、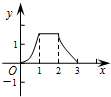 |
查看答案和解析>>
科目:初中数学 来源: 题型:
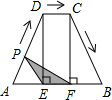 (2013•河北)如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,且AE=EF=FB=5,DE=12动点P从点A出发,沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止.设运动时间为t秒,y=S△EPF,则y与t的函数图象大致是( )
(2013•河北)如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,且AE=EF=FB=5,DE=12动点P从点A出发,沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止.设运动时间为t秒,y=S△EPF,则y与t的函数图象大致是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•道外区二模)如图,在平面直角坐标系中,直线y=x+b与x轴交于点A,与正比例函数y=-
(2012•道外区二模)如图,在平面直角坐标系中,直线y=x+b与x轴交于点A,与正比例函数y=-| 4 | 3 |
查看答案和解析>>
科目:初中数学 来源:新课程同步练习 数学 八年级上册 题型:044
如图,阅读函数图象,并根据你所获得的信息回答问题:
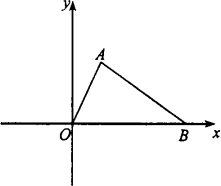
(1)折线OAB表示某个具体问题的函数图象,请你编写出一道符合图象意义的应用题.
(2)根据你所给出的应用题分别指出x轴,y轴所表示的意义,并写出A、B两点的坐标.
(3)求出图象中直线AB的函数解析式,并注明自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
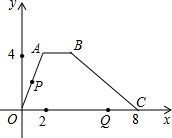 如图,在平面直角坐标系中,点A,B在第一象限,AB∥x轴,AB=2,点Q(6,0),根据图象回答:
如图,在平面直角坐标系中,点A,B在第一象限,AB∥x轴,AB=2,点Q(6,0),根据图象回答:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com