
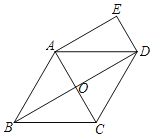
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=2,∠BCD=120°,求四边形AODE的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据菱形的性质得出AC⊥BD,再根据平行四边形的判定定理得四边形AODE为平行四边形,由矩形的判定定理得出四边形AODE是矩形;
(2)证明△ABC是等边三角形,得出OA=1,由勾股定理得出OB=![]() ,由菱形的性质得出OD=OB=
,由菱形的性质得出OD=OB=![]() ,即可求出四边形AODE的面积.
,即可求出四边形AODE的面积.
(1)证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴∠AOD=90°,
∴四边形AODE是矩形;
(2)解:∵∠BCD=120°,AB∥CD,
∴∠ABC=180°﹣120°=60°,
∵AB=BC=2,
∴△ABC是等边三角形,
∴OA=![]() ×2=1,
×2=1,
∵在菱形ABCD中,AC⊥BD
∴由勾股定理OB=![]() ,
,
∵四边形ABCD是菱形,
∴OD=OB=![]() ,
,
∴四边形AODE的面积=OAOD=![]() .
.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】根据以下信息,解答下列问题.

(1)小华同学设乙型机器人每小时搬运xkg产品,可列方程为 .
小惠同学设甲型机器人搬运800kg所用时间为y小时,可列方程为 .
(2)请你按照(1)中小华同学的解题思路,写出完整的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
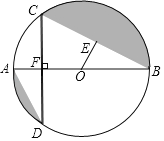
【题目】如图,AB为⊙O直径,OE⊥BC垂足为E,AB⊥CD垂足为F.
(1)求证:AD=2OE;
(2)若∠ABC=30°,⊙O的半径为2,求两阴影部分面积的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
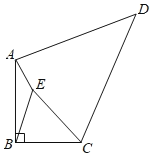
【题目】如图,在四边形ABCD中,∠B=90°,∠D=45°,AB=BC=2,点E为四边形ABCD内部一点,且满足CE2﹣AE2=2BE2,则点E在运动过程中所形成的图形的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
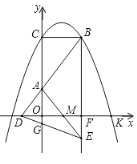
【题目】如图,![]() 与
与![]() 轴交于点C,与
轴交于点C,与![]() 轴的正半轴交于点K,过点
轴的正半轴交于点K,过点![]() 作
作![]() 轴交抛物线于另一点B,点
轴交抛物线于另一点B,点![]() 在
在![]() 轴的负半轴上,连结
轴的负半轴上,连结![]() 交
交![]() 轴于点A,若
轴于点A,若![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)当![]() 时,判断点
时,判断点![]() 是否落在抛物线上,并说明理由;
是否落在抛物线上,并说明理由;
(3)过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() 延长
延长![]() 至
至![]() ,使得
,使得![]() 连结
连结![]() 交
交![]() 轴于点
轴于点![]() 连结AE交
连结AE交![]() 轴于点
轴于点![]() 若
若![]() 的面积与
的面积与![]() 的面积之比为
的面积之比为![]() 则求出抛物线的解析式.
则求出抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形 ABCD 中, P 为 AB 的中点,![]() 的延长线于点 E ,连接 AE 、 BE ,
的延长线于点 E ,连接 AE 、 BE ,![]() 交 DP 于点 F ,连接 BF 、FC ,下列结论:①
交 DP 于点 F ,连接 BF 、FC ,下列结论:① ![]() ;② FB AB ;③
;② FB AB ;③ ![]() ;④ FC EF . 其中正确的是( )
;④ FC EF . 其中正确的是( )
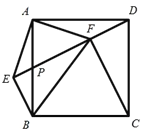
A.①②④B.①③④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t s,解答下列问题:
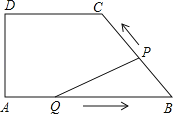
(1)当t为何值时,P,Q两点同时停止运动;
(2)设△PQB的面积为S,当t为何值时,S取得最大值,并求出最大值;
(3)当△PQB为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知C为线段AB中点,∠ACM=α.Q为线段BC上一动点(不与点B重合),点P在射线CM上,连接PA,PQ,记BQ=kCP.
(1)若α=60°,k=1,
①如图1,当Q为BC中点时,求∠PAC的度数;
②直接写出PA、PQ的数量关系;
(2)如图2,当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com