
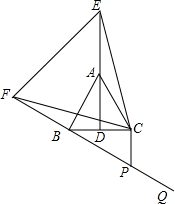
 如图,在等边△ABC中,已知AD是∠BAC的角平分线,E为AD延长线上一点,以CE为一边且在CE以左作等边△CEF,连接BF.
如图,在等边△ABC中,已知AD是∠BAC的角平分线,E为AD延长线上一点,以CE为一边且在CE以左作等边△CEF,连接BF.分析 (1)只要证明△FCB≌△ECA即可;
(2)由△FCB≌△ECA,可知S△BCF=S△AEC,推出S四边形EFDB=S四边形EFBC-S△EDC=S△EFC+S△BCF-(S△AEC+S△ADC)=S△EFC-S△ADC,由此即可解决问题;
(3)作CH⊥PF于H.由△FCB≌△ECA,推出∠EAC=∠FBC=150°,推出∠CBH=30°,解直角三角形即可解决问题;
解答 (1)证明:∵△ABC,△CEF都是等边三角形,
∴CB=CA,CF=CE,∠ACB=∠ECF,
∴∠FCB=∠ECA,
∴△FCB≌△ECA,
∴BF=AE.
(2)解:∵AB=AC,AD平分∠BAC,
∴AD⊥BC,BD=CD=4,
∵△FCB≌△ECA,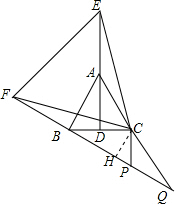
∴S△BCF=S△AEC,
∵S四边形EFDB=S四边形EFBC-S△EDC
=S△EFC+S△BCF-(S△AEC+S△ADC)
=S△EFC-S△ADC
=$\frac{\sqrt{3}}{4}$×152-$\frac{1}{2}$×4×4$\sqrt{3}$
=$\frac{193}{4}$$\sqrt{3}$.
(3)解:作CH⊥PF于H.
∵△FCB≌△ECA,
∴∠EAC=∠FBC=150°,
∴∠CBH=30°,
∴CH=$\frac{1}{2}$BC=4,
在Rt△CHP中,PH=$\sqrt{P{C}^{2}-C{H}^{2}}$=3,
在Rt△CHP中,CH=4,HQ=HP+PQ=3+5=8,
∴CQ=$\sqrt{C{H}^{2}+H{Q}^{2}}$=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$.
点评 本题考查全等三角形的性质、等边三角形的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会用转化的思想思考问题,学会添加常用辅助线,构造直角三角形,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
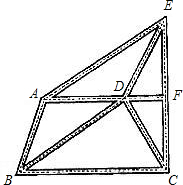 已知:如图是某城市部分街道示意图,AF∥BC,且AF⊥CE,AB=DC,AB∥DE,BD∥AE.甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F,乙乘2路车,路线是B→D→C→F,假设两车速度相同,途中耽误时间相同,那么谁先到达F站?说明理由.
已知:如图是某城市部分街道示意图,AF∥BC,且AF⊥CE,AB=DC,AB∥DE,BD∥AE.甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F,乙乘2路车,路线是B→D→C→F,假设两车速度相同,途中耽误时间相同,那么谁先到达F站?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
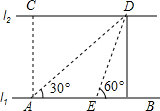 如图,河的两岸l1与l2互相平行,A、B是l1上的两点,C、D是l2上的两点,某同学在A处测得∠CAB=90°,∠DAB=30°,再沿AB方向走20米到达点E(即AE=20),测得∠DEB=60°.
如图,河的两岸l1与l2互相平行,A、B是l1上的两点,C、D是l2上的两点,某同学在A处测得∠CAB=90°,∠DAB=30°,再沿AB方向走20米到达点E(即AE=20),测得∠DEB=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某校把一块三角形的废地ABC改建成一个花园,测得AC=80cm,BC=60cm,AB=100cm.
如图,某校把一块三角形的废地ABC改建成一个花园,测得AC=80cm,BC=60cm,AB=100cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{360}{x}$=$\frac{360}{x-3}$+6 | B. | $\frac{360}{x}$=$\frac{360}{x+3}$+6 | C. | $\frac{360}{x-3}$=$\frac{360}{x}$+6 | D. | $\frac{360}{x+3}$=$\frac{360}{x}$+6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
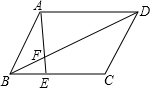 如图,点E是平行四边形ABCD边BC上一点,BE:EC=4:1,AE交BD于F点,BF:FD等于( )
如图,点E是平行四边形ABCD边BC上一点,BE:EC=4:1,AE交BD于F点,BF:FD等于( )| A. | 4:5 | B. | 4:9 | C. | 5:9 | D. | 4:10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com