
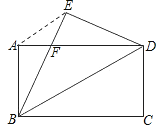
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连接AE.
求证:(1)BF=DF;
(2)AE∥BD;
(3)若AB=6,AD=8,求BF的长.
【答案】(1)证明见解析;(2)证明见解析;(3)BF的长为 ![]() .
.
【解析】试题分析:(1)由矩形的性质和折叠的性质可得到∠ADB=∠EBD,从而得BF=DF;
(2)根据矩形的性质和三角形内角可得∠AEB=∠FBD,再根据平行线的判定即可得;
(3)在Rt△ABF中 ,设BF=FD=![]() ,则AF
,则AF ![]() ,利用勾股定理即可得.
,利用勾股定理即可得.
试题解析:(1)在矩形ABCD中,AD∥BC,AD=BC,∴ ∠DBC=∠ADB,
∵ ∠DBC=∠EBD ,∴ ∠ADB=∠EBD,∴ BF=FD;
(2)∵ AD=BC=BE ,BF=DF ,∴ AF=EF,∴ ∠AEB=∠EAF,
∵ ∠AFE=∠BFD ,∠FBD=∠FDB,∴ ∠AEB=∠EBD, ∴ AE∥BD;
(3)在Rt△ABF中 ,设BF=FD=![]() ,则AF
,则AF ![]() ,则
,则
![]() ,解得:
,解得: ![]() , ∴ BF的长为
, ∴ BF的长为 ![]() .
.


科目:初中数学 来源: 题型:
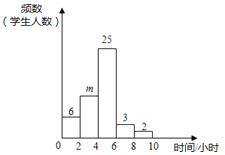
【题目】小强对自己所在班级的48名学生平均每周参加课外活动的时间进行了调查,由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
(1)求m的值;
(2)从参加课外活动时间在6~10小时的5名学生中随机选取2人,请你用列表或画树状图的方法,求其中至少有1人课外活动时间在8~10小时的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
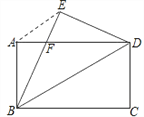
【题目】如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F。
(1)求证:△ABE≌△FCE;
(2)连接AC、BF,若AE=![]() BC,求证:四边形ABFC为矩形;
BC,求证:四边形ABFC为矩形;
(3)在(2)条件下,当△ABC再满足一个什么条件时,四边形ABFC为正方形。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是 ( )

A. ![]() B. 2
B. 2![]() C. 3 D. 2
C. 3 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知一次函数y=3﹣2x的图象经过P1(x1 , y1),P2(x2 , y2)两点,若x1<x2 , 则y1y2 . (填“>”,“<”或“=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形统计图(如图①)和条形统计图(如图②),经确认扇形统计图是正确的,而条形统计图尚有一处错误.
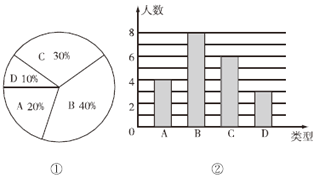
回答下列问题:
(1)写出条形统计图中存在的错误,并说明理由.
(2)写出这20名学生每人植树量的众数、中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com