
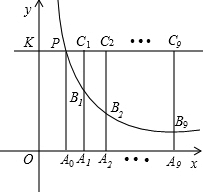
 如图,直线y=k和双曲线y=
如图,直线y=k和双曲线y=| k |
| x |
| k |
| x |
| C9B9 |
| A9B9 |
| k |
| x |
| k |
| x |
| k |
| 10 |
| C9B9 |
| A9B9 |
| k |
| x |
| k |
| x |
| k |
| x |
| k |
| 10 |
| k |
| 10 |
| 9 |
| 10 |
| k |
| 10 |
| C9B9 |
| A9B9 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
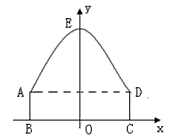
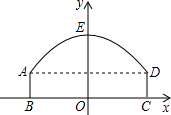 线段BC的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
线段BC的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.查看答案和解析>>
科目:初中数学 来源: 题型:
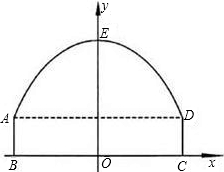 以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系.y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系.y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.查看答案和解析>>
科目:初中数学 来源: 题型:
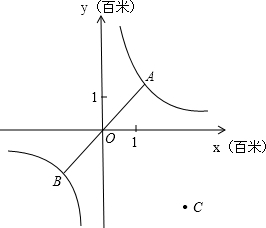 如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于点O,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=
如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于点O,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=| 4 | x |
查看答案和解析>>
科目:初中数学 来源:安徽省期末题 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《二次函数》(05)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com