
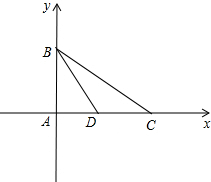
 坐标系(如图).
坐标系(如图). 解:(1)∵AB=AC=4,BD是AC边上的中线,
解:(1)∵AB=AC=4,BD是AC边上的中线,
|
|
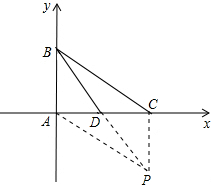 由题意得,AD=DC,
由题意得,AD=DC,| ∥ |
. |


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:
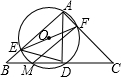 如图,已知△ABC为等腰直角三角形,D为斜边BC的中点,经过点A、D的⊙O与边AB、AC、BC分别相交于点E、F、M.对于如下五个结论:①∠FMC=45°;②AE+AF=AB;③
如图,已知△ABC为等腰直角三角形,D为斜边BC的中点,经过点A、D的⊙O与边AB、AC、BC分别相交于点E、F、M.对于如下五个结论:①∠FMC=45°;②AE+AF=AB;③| ED |
| EF |
| BA |
| BC |
| A、2个 | B、3个 | C、4个 | D、5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知△ABC中,AB=10cm,AC=8cm,BC=6cm,如果点P由B出发沿BA方向向点A匀速运动,速度为2cm/s,同时点Q由A出发沿AC方向向点C匀速运动,速度为1cm/s,连接PQ,设运动的时间为t(单位:s)(0≤t≤5).解答下列问题:
如图,已知△ABC中,AB=10cm,AC=8cm,BC=6cm,如果点P由B出发沿BA方向向点A匀速运动,速度为2cm/s,同时点Q由A出发沿AC方向向点C匀速运动,速度为1cm/s,连接PQ,设运动的时间为t(单位:s)(0≤t≤5).解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 22、(1)小方格中△ABC沿BA方向平移,平移的距离为线段AB的2倍;
22、(1)小方格中△ABC沿BA方向平移,平移的距离为线段AB的2倍;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com