
 为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:
为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求: ,又∵抛物线关于y轴对称,
,又∵抛物线关于y轴对称,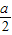 ,a),F(
,a),F(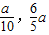 )代入y=-x2+c得:
)代入y=-x2+c得: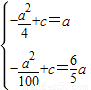 ,
,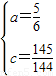 .
.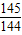 .
. BC=
BC=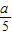 ,
,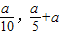 ).
).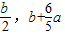 ),
), ,代入y=-x2+
,代入y=-x2+
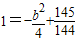
 .
.

科目:初中数学 来源: 题型:
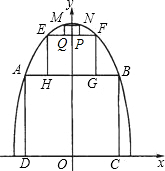 为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:
为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(50):2.3 二次函数的应用(解析版) 题型:解答题
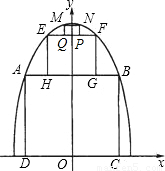 为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:
为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:查看答案和解析>>
科目:初中数学 来源:第26章《二次函数》中考题集(48):26.3 实际问题与二次函数(解析版) 题型:解答题
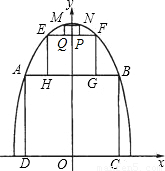 为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:
为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:查看答案和解析>>
科目:初中数学 来源:第20章《二次函数和反比例函数》中考题集(47):20.5 二次函数的一些应用(解析版) 题型:解答题
 为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:
为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com