
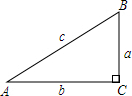
 已知,在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c.
已知,在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c.分析 (1)根据锐角三角函数的定义可以表示出sinA、cosA,根据勾股定理得到三边的关系,从而可以证明结论成立;
(2)根据锐角三角函数的定义可以分别表示出sinA、cosA、tanA,从而可以得到它们之间的关系;
(3)根据(2)中的结论可以得到tanα的值.
解答 (1)证明:∵在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,
∴sinA=$\frac{a}{c}$,cosA=$\frac{b}{c}$,a2+b2=c2.
∴$si{n}^{2}A+co{s}^{2}A=\frac{{a}^{2}}{{c}^{2}}+\frac{{b}^{2}}{{c}^{2}}=\frac{{a}^{2}+{b}^{2}}{{c}^{2}}$=$\frac{{c}^{2}}{{c}^{2}}=1$.
即sin2A+cos2A=1.
(2)解:∵在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,
∴sinA=$\frac{a}{c}$,cosA=$\frac{b}{c}$,tanA=$\frac{a}{b}$.
∴$\frac{sinA}{cosA}=\frac{\frac{a}{c}}{\frac{b}{c}}=\frac{a}{b}=tanA$.
即sinA,cosA与tanA之间的关系是:tanA=$\frac{sinA}{cosA}$.
(3)解:∵$\frac{sinα+cosα}{2sinα+cosα}$=$\frac{2}{3}$,
∴$\frac{\frac{sinα}{cosα}+\frac{cosα}{cosα}}{2×\frac{sinα}{cosα}+\frac{cosα}{cosα}}=\frac{tanα+1}{2tanα+1}=\frac{2}{3}$.
解得,tanα=1.
故答案为:1.
点评 本题考查解直角三角形,解题的关键是明确锐角三角函数,找出所求问题需要的条件.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知C、D是线段AB上的两点,且AC=$\frac{1}{3}$AB,BD=$\frac{1}{3}$BC,图中一共有6条线段,若AC=3,则CD的长度为4.
如图,已知C、D是线段AB上的两点,且AC=$\frac{1}{3}$AB,BD=$\frac{1}{3}$BC,图中一共有6条线段,若AC=3,则CD的长度为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com