
如图1,已知直线y=kx与抛物线y=-![]() x2+
x2+![]() 交于点A(3,6).
交于点A(3,6).
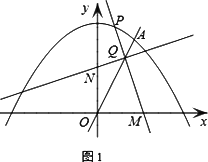
(1)求直线y=kx的解析式和线段OA的长度;
(2)点P为抛物线第一象限内的动点,过点P作直线PM,交x轴于点M(点M、O不重合),交直线OA于点Q,再过点Q作直线PM的垂线,交y轴于点N.试探究:线段QM与线段QN的长度之比是否为定值?如果是,求出这个定值;如果不是,说明理由;
(3)如图2,若点B为抛物线上对称轴右侧的点,点E在线段OA上(与点O、A不重合),点D(m,0)是x轴正半轴上的动点,且满足∠BAE=∠BED=∠AOD.继续探究:m在什么范围时,符合条件的E点的个数分别是1个、2个?
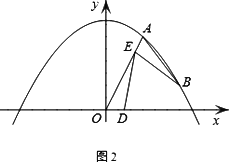
|
解:(1)把点A(3,6)代入y=kx得; ∵6=3k, ∴k=2, ∴y=2x.(2012金华市) OA= (2) 如答图1,过点Q作QG⊥y轴于点G,QH⊥x轴于点H. ①当QH与QM重合时,显然QG与QN重合, 此时 ②当QH与QM不重合时, ∵QN⊥QM,QG⊥QH 不妨设点H,G分别在x、y轴的正半轴上, ∴∠MQH=∠GQN, 又∵∠QHM=∠QGN=90° ∴△QHM∽△QGN(5分), ∴ 当点P、Q在抛物线和直线上不同位置时,同理可得 (3)如答图2,延长AB交x轴于点F,过点F作FC⊥OA于点C,过点A作AR⊥x轴于点R ∵∠AOD=∠BAE, ∴AF=OF, ∴OC=AC= ∵∠ARO=∠FCO=90°,∠AOR=∠FOC, ∴△AOR∽△FOC, ∴ ∴OF= ∴点F( 设点B(x, 过点B作BK⊥AR于点K,则△AKB∽△ARF, ∴ 即 解得x1=6,x2=3(舍去), ∴点B(6,2), ∴BK=6-3=3,AK=6-2=4, ∴AB=5(8分); (求AB也可采用下面的方法) 设直线AF为y=kx+b(k≠0)把点A(3,6),点F( k= ∴ ∴ ∴ ∴B(6,2), ∴AB=5(8分)(其它方法求出AB的长酌情给分) 在△ABE与△OED中 ∵∠BAE=∠BED, ∴∠ABE+∠AEB=∠DEO+∠AEB, ∴∠ABE=∠DEO, ∵∠BAE=∠EOD, ∴△ABE∽△OED.(9分) 设OE=x,则AE= 由△ABE∽△OED得 ∴ ∴ ∴顶点为( 如答图3,当 当 ∴当 当
|
|
二次函数综合题. |


科目:初中数学 来源:浙江省义乌市2012年初中毕业生学业考试数学试题 题型:044
如图1,已知直线y=kx与抛物线y=-![]() x2+
x2+![]() 交于点A(3,6).
交于点A(3,6).

(1)求直线y=kx的解析式和线段OA的长度;
(2)点P为抛物线第一象限内的动点,过点P作直线PM,交x轴于点M(点M、O不重合),交直线OA于点Q,再过点Q作直线PM的垂线,交y轴于点N.试探究:线段QM与线段QN的长度之比是否为定值?如果是,求出这个定值,如果不是,说明理由;
(3)如图2,若点B为抛物线上对称轴右侧的点,点E在线段OA上(与点O、A不重合),点D(m,0)是x轴正半轴上的动点,且满足∠BAE=∠BED=∠AOD.继续探究:m在什么范围时,符合条件的E点的个数分别是1个、2个?
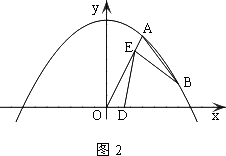
查看答案和解析>>
科目:初中数学 来源:2007年江苏地区数学中考动态型试题-新人教 题型:044
如图甲,已知直线y=2x(即直线l1)和直线![]() (即直线l2),l2与x轴相交于点A.点P从原点O出发,向x轴的正方向作匀速运动,速度为每秒1个单位,同时点Q从A点出发,向x轴的负方向作匀速运动,速度为每秒2个单位.设运动了t秒.
(即直线l2),l2与x轴相交于点A.点P从原点O出发,向x轴的正方向作匀速运动,速度为每秒1个单位,同时点Q从A点出发,向x轴的负方向作匀速运动,速度为每秒2个单位.设运动了t秒.

(1)求这时点P、Q的坐标(用t表示).
(2)过点P、Q分别作x轴的垂线,与l1、l2分别相交于点O1、O2(如图乙).
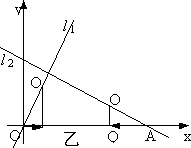
①以O1为圆心、O1P为半径的圆与以O2为圆心、O2Q为半径的圆能否相切?若能,求出t值;若不能,说明理由.
②以O1为圆心、P为一个顶点的正方形与以O2为中心、Q为一个顶点的正方形能否有无数个公共点?若能,求出t值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源:2013届江苏省无锡市前洲中学九年级下学期期中考试数学试卷(带解析) 题型:解答题
阅读下列材料:
我们知道,一次函数y=kx+b的图象是一条直线,而y=kx+b经过恒等变形可化为直线的另一种表达形式:Ax+Bx+C=0(A、B、C是常数,且A、B不同时为0).如图1,点P(m,n)到直线l:Ax+Bx+C=0的距离(d)计算公式是:d=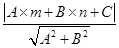 .
.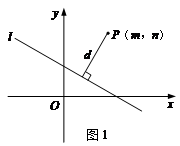
例:求点P(1,2)到直线y=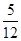 x-
x- 的距离d时,先将y=
的距离d时,先将y=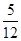 x-
x- 化为5x-12y-2=0,再由上述距离公式求得d=
化为5x-12y-2=0,再由上述距离公式求得d=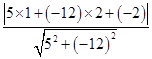 =
=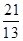 .
.
解答下列问题:
如图2,已知直线y=- x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).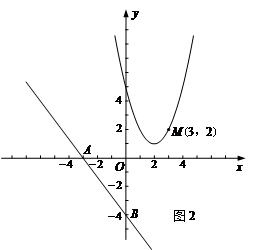
(1)求点M到直线AB的距离.
(2)抛物线上是否存在点P,使得△PAB的面积最小?若存在,求出点P的坐标及△PAB面积的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省无锡市九年级下学期期中考试数学试卷(解析版) 题型:解答题
阅读下列材料:
我们知道,一次函数y=kx+b的图象是一条直线,而y=kx+b经过恒等变形可化为直线的另一种表达形式:Ax+Bx+C=0(A、B、C是常数,且A、B不同时为0).如图1,点P(m,n)到直线l:Ax+Bx+C=0的距离(d)计算公式是:d= .
.

例:求点P(1,2)到直线y=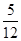 x-
x-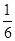 的距离d时,先将y=
的距离d时,先将y=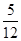 x-
x-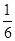 化为5x-12y-2=0,再由上述距离公式求得d=
化为5x-12y-2=0,再由上述距离公式求得d=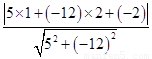 =
= .
.
解答下列问题:
如图2,已知直线y=-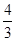 x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).

(1)求点M到直线AB的距离.
(2)抛物线上是否存在点P,使得△PAB的面积最小?若存在,求出点P的坐标及△PAB面积的最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com