
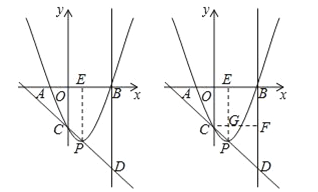
【题目】已知二次函数![]() (a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B且垂直于x轴的直线交于点D,且CP:PD=2:3.
(a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B且垂直于x轴的直线交于点D,且CP:PD=2:3.

(1)求A、B两点的坐标;
(2)若tan∠PDB=![]() ,求这个二次函数的关系式.
,求这个二次函数的关系式.
【答案】(1)A(![]() ,0);(2)
,0);(2)![]() .
.
【解析】
试题分析:(1)由二次函数的解析式可求出对称轴为x=1,过点P作PE⊥x轴于点E,所以OE:EB=CP:PD;
(2)过点C作CF⊥BD于点F,交PE于点G,构造直角三角形CDF,利用tan∠PDB=![]() 即可求出FD,由于△CPG∽△CDF,所以可求出PG的长度,进而求出a的值,最后将A(或B)的坐标代入解析式即可求出c的值.
即可求出FD,由于△CPG∽△CDF,所以可求出PG的长度,进而求出a的值,最后将A(或B)的坐标代入解析式即可求出c的值.
试题解析:(1)过点P作PE⊥x轴于点E,∵![]() ,∴该二次函数的对称轴为:x=1,∴OE=1,∵OC∥BD,∴CP:PD=OE:EB,∴OE:EB=2:3,∴EB=
,∴该二次函数的对称轴为:x=1,∴OE=1,∵OC∥BD,∴CP:PD=OE:EB,∴OE:EB=2:3,∴EB=![]() ,∴OB=OE+EB=
,∴OB=OE+EB=![]() ,∴B(
,∴B(![]() ,0).∵A与B关于直线x=1对称,∴A(
,0).∵A与B关于直线x=1对称,∴A(![]() ,0);
,0);
(2)过点C作CF⊥BD于点F,交PE于点G,令x=1代入![]() ,∴y=c﹣a,令x=0代入
,∴y=c﹣a,令x=0代入![]() ,∴y=c,∴PG=a,∵CF=OB=
,∴y=c,∴PG=a,∵CF=OB=![]() ,∴tan∠PDB=
,∴tan∠PDB=![]() ,∴FD=2,∵PG∥BD,∴△CPG∽△CDF,∴
,∴FD=2,∵PG∥BD,∴△CPG∽△CDF,∴![]() ,∴PG=
,∴PG=![]() ,∴a=
,∴a=![]() ,∴
,∴![]() ,把A(
,把A(![]() ,0)代入
,0)代入![]() ,∴解得:c=﹣1,∴该二次函数解析式为:
,∴解得:c=﹣1,∴该二次函数解析式为:![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格中,点![]() 、
、![]() 、
、![]() 在小正方形的顶点上.
在小正方形的顶点上.

(1)在图中画出与![]() 关于直线
关于直线![]() 成轴对称的
成轴对称的![]() ;
;
(2)在直线![]() 上找一点
上找一点![]() ,使
,使![]() 的值最小;
的值最小;
(3)若![]() 是以
是以![]() 为腰的等腰三角形,点
为腰的等腰三角形,点![]() 在
在![]() 图中小正方形的顶点上.这样的点
图中小正方形的顶点上.这样的点![]() 共有_______个.(标出位置)
共有_______个.(标出位置)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.
(1)求证:CA=CN;
(2)连接DF,若cos∠DFA=![]() ,AN=
,AN=![]() ,求圆O的直径的长度.
,求圆O的直径的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD中AB= 3,点B在边CD上,且 CD=3DE. 将△ADE沿AE对折至△AFE,延长EF交边BC 于点G,连接AG,CF下列结论:①点G是BC的中点;②FG=FC;③![]() GAE=45;④GE=BG+DE.其中正确的是( )
GAE=45;④GE=BG+DE.其中正确的是( )

A. ①② B. ①③④ C. ②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道对于x轴上的任意两点A(x1,0),B(x2,0),有AB=|x1﹣x2|,而对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1﹣x2|+|y1﹣y2|称为Pl,P2两点间的直角距离,记作d(P1,P2),即d(P1,P2)=|x1﹣x2|+|y1﹣y2|.
(1)已知O为坐标原点,若点P坐标为(1,3),则d(O,P)= ;
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=2,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(3)试求点M(2,3)到直线y=x+2的最小直角距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com