
【题目】图![]() 是一个长为
是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线剪开分成四块小长方形,然后按图
的长方形,沿图中虚线剪开分成四块小长方形,然后按图![]() 的形状拼成一个正方形.(
的形状拼成一个正方形.(![]() )
)
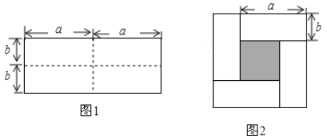
(1)图2的阴影部分的正方形的边长是____.
(2)用两种不同的方法求图中阴影部分的面积.
(方法![]() )
)![]() 阴影=____________________;
阴影=____________________;
(方法![]() )
)![]() 阴影=____________________;
阴影=____________________;
(3)利用(方法![]() )(方法
)(方法![]() )中两个代数式之间存在的等量关系,解决问题:若
)中两个代数式之间存在的等量关系,解决问题:若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;
;![]() (3)
(3)![]()
【解析】
(1)观察图2可知:阴影部分的正方形的边长是(a-b);
(2)【方法![]() 】图2中阴影部分为边长为(a-b)的正方形,利用正方形的面积公式可得出S阴影=(a-b)2;【方法
】图2中阴影部分为边长为(a-b)的正方形,利用正方形的面积公式可得出S阴影=(a-b)2;【方法![]() 】图2中阴影部分可看成在边长为(a+b)的正方形中减去4个长为a、宽为b的长方形,利用正方形及长方形的面积公式可得出S阴影=(a+b)2-4ab;
】图2中阴影部分可看成在边长为(a+b)的正方形中减去4个长为a、宽为b的长方形,利用正方形及长方形的面积公式可得出S阴影=(a+b)2-4ab;
(3)由阴影部分的面积相等可得出:(a+b)2-4ab=(a-b)2;据此可得出(x-y)2=(x+y)2-4xy,代入![]() 即可得出结论.
即可得出结论.
解:(1)根据题意得:图2的阴影部分的正方形的边长是(a-b).
故答案为:a-b;
(2)【方法![]() 】图2中阴影部分为边长为(a-b)的正方形,
】图2中阴影部分为边长为(a-b)的正方形,
∴S阴影=(a-b)2;
【方法![]() 】图2中阴影部分可看成在边长为(a+b)的正方形中减去4个长为a、宽为b的长方形,
】图2中阴影部分可看成在边长为(a+b)的正方形中减去4个长为a、宽为b的长方形,
∴S阴影=(a+b)2-4ab.
故答案为:(a-b)2;(a+b)2-4ab.
(3)由(2)可知:(a+b)2-4ab=(a-b)2.
∴(x-y)2=(x+y)2-4xy
=102-4×16,
=36,
∴x-y =![]() ,
,


科目:初中数学 来源: 题型:
【题目】如图,把![]() 张形状大小完全相同的小长方形卡片不重叠地放在一个底面为长方形的盒子底部,盒子底面未被覆盖的部分用阴影部分表示则图中两块阴影部分的周长的和是( )
张形状大小完全相同的小长方形卡片不重叠地放在一个底面为长方形的盒子底部,盒子底面未被覆盖的部分用阴影部分表示则图中两块阴影部分的周长的和是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若OC是∠AOB内部的一条射线,则下列式子中,不能表示“OC是∠AOB的平分线”的是( )
A. ∠AOC=∠BOC B. ∠AOB=2∠BOC
C. ∠AOC=![]() ∠AOB D. ∠AOC+∠BOC=∠AOB
∠AOB D. ∠AOC+∠BOC=∠AOB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张上星期六买进某公司的股票2000股,每股30元,下表是本周内每日该股票的涨跌情况(单位:元):
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
每股涨跌 |
|
|
|
|
|
|
(1)星期三收盘时,每股是多少元?
(2)本周内最高价是每股多少元?
(3)请用拆线统计图表示该股票这六天的涨跌情况.(请在已设计好的坐标纸里画图)
(4)已知小张买过股票时付了1.5‰的手续费,卖出时需付成交额1.5‰的手续费和1‰的交易税,如小张在星期六收盘时将股票全部卖出,它的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=3.当四边形BDEF的周长最小时,点E的坐标是( )
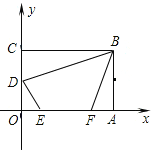
A. (![]() ,0) B. (1,0) C. (
,0) B. (1,0) C. (![]() ,0) D. (2,0)
,0) D. (2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某巡警骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶情况记录如下(单位:千米):
+10,﹣8,+7,﹣15,+6,﹣16,+4,﹣2
(1)A处在岗亭何方?距离岗亭多远?
(2)若摩托车每行驶1千米耗油a升,这一天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
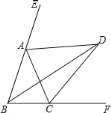
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°∠ABD;④BD平分∠ADC;⑤∠BDC=![]() ∠BAC.其中正确的结论有__________(填序号)
∠BAC.其中正确的结论有__________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】松雷中学刚完成一批校舍的修建,有一些相同的办公室需要粉刷墙面.一天3名一级技工去粉刷7个办公室,结果其中有90m2墙面未来得及粉刷;同样时间内4名二级技工粉刷了7个办公室之外,还多粉刷了另外的70m2墙面.每名一级技工比二级技工一天多粉刷40m2墙面.
(1)求每个办公室需要粉刷的墙面面积.
(2)已知每名一级技工每天需要支付费用100元,每名二级技工每天需要支付费用90元.松雷中学有40个办公室的墙面和720m2的展览墙需要粉刷,现有3名一级技工的甲工程队,4名二级技工的乙工程队,要来粉刷墙面.松雷中学有两个选择方案,方案一:全部由甲工程队粉刷;方案二:全部由乙工程队粉刷;若使得总费用最少,松雷中学应如何选择方案,请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠B=30°,AC=3cm,点P在边AC上以1cm/s的速度从点A向终点C运动,与此同时点Q在边AB上以同样的速度从点B向终点A运动,各自到达终点后停止运动,设运动时间为t(s),则当△APQ是直角三角形时,t的值为( )
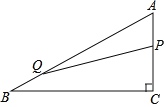
A.2sB.4sC.2s或4sD.2s或4.5s
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com