
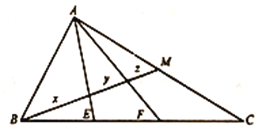
【题目】在![]() 中,
中,![]() 、
、![]() 是
是![]() 边上的三等分点,
边上的三等分点,![]() 是
是![]() 边上的中线,
边上的中线,![]() 、
、![]() 分
分![]() 为三段的长分别是
为三段的长分别是![]() 、
、![]() 、
、![]() ,若这三段有
,若这三段有![]() ,则
,则![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
设BM分别交AE,AF于P,Q,连接MF, 作FH//BM交AC于H,根据中点的性质可得EP//MF,根据BE=EF,得到BP=PM,根据平行线分线段成比例定理可得CF:CB=FH:BM=CH:CM=1:3,则FH:QM=AH:AM=5:3, 设FH=t,所以BM=3t,QM=0.6t,BP=1.5t,
PQ=0.9t,即可求解.
设BM分别交AE,AF于P,Q,连接MF,
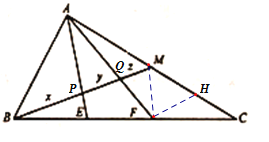
因为MF//AE,所以EP//MF,又因为BE=EF,所以BP=PM
作FH//BM交AC于H,CF:CB=FH:BM=CH:CM=1:3,
![]() FH:QM=AH:AM=5:3,
FH:QM=AH:AM=5:3,
设FH=t,所以BM=3t,QM=0.6t,BP=1.5t,PQ=0.9t
所以BP:PQ:QM=5:3:2
即x:y:z=5:3:2
故选:D.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
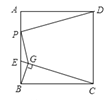
【题目】如图,已知正方形ABCD的边长是4,点E是AB边上一动点,连接CE,过点B作BG⊥CE于点G,点P是AB边上另一动点,则PD+PG的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt⊿ABC中,∠C = 90,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=6,OC=![]() ,则直角边BC的长为___________
,则直角边BC的长为___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】共享单车为大众出行提供了方便,如图为单车实物图,如图为单车示意图,AB与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线BE方向调节.已知,∠ABE=70°,∠EAB=45°,车轮半径为0.3m,BE=0.4m.小明体验后觉得当坐垫C离地面高度为0.9m时骑着比较舒适,求此时CE的长.(结果精确到1cm)参考数据:sin70.≈0.94,cos70.≈0.34,tan70.≈2.75,![]() ≈1.41
≈1.41

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,且
点,且![]() .
.

(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)判断![]() 的形状,证明你的结论;
的形状,证明你的结论;
(3)点![]() 是
是![]() 轴上的一个动点,当
轴上的一个动点,当![]() 的值最小时,求
的值最小时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=![]() .下列结论:
.下列结论:
①△ADE∽△ACD; ②当BD=6时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD为8; ④0<CE≤6.4.

其中正确的结论是____________.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在小正方形的边长均为1的方格纸中,有线段![]() 和线段
和线段![]() ,点
,点![]() 均在小正方形的顶点上.
均在小正方形的顶点上.
(1)在方格纸中画出以![]() 为斜边的直角三角形
为斜边的直角三角形![]() ,点E在小正方形的顶点上,且
,点E在小正方形的顶点上,且![]() 的面积为5;
的面积为5;
(2)在方格纸中画出以![]() 为一边的
为一边的![]() ,点
,点![]() 在小正方形的顶点上,
在小正方形的顶点上,![]() 的面积为4,射线
的面积为4,射线![]() 与射线
与射线![]() 交于点
交于点![]() ,且
,且![]() ,连接
,连接![]() ,请直接写出线段
,请直接写出线段![]() 的长.
的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com