
【题目】 如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C,D两点,D点在x轴下方且横坐标小于3,则下列结论:①a﹣b+c<0;②2a+b+c>0;③x(αx+b)≤a+b;④a>﹣1.其中正确的有( )
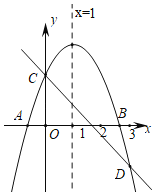
A.4个B.3个C.2个D.1个
【答案】B
【解析】
根据二次函数的图象与性质得出对称轴为x=1则得出点(3,y)关于直线x=1对称的点为(﹣1,y)然后即可得出①正确,令y=0代入y=﹣x+c得出c,再根据函数图象知道1<c<2结合对称轴得出②正确,根据函数图象判断③即可,联立抛物线与一次函数的方程然后化简判断④的对错.
解:①由图象可知:抛物线的对称轴为x=1时,
∴点(3,y)关于直线x=1对称的点为(﹣1,y),
∵x=3时,y<0,
∴x=﹣1,y<0
∴a﹣b+c<0,故①正确;
②令y=0代入y=﹣x+c,
∴x=c,
由图象可知:1<c<2,
由图象可知:![]() =1,
=1,
∴2a+b=0,
∴2a+b+c=c>0,故②正确;
③由图象可知:x=1时,y的最大值为a+b+c,
∴当x取全体实数时,ax2+bx+c≤a+b+c,
即x(ax+b)≤a+b,故③正确;
④联立![]() ,
,
化简得:ax2+(b+1)x=0,
∴x=0或x=![]() ,
,
即D的横坐标为![]() ,
,
由于b=﹣2a,a<0,且![]() <3,
<3,
∴﹣b﹣1>3a,
∴a<﹣1,故④错误,
故选:B.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
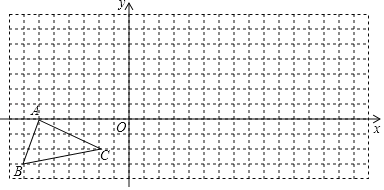
【题目】如图,△ABC在方格纸中,设单元正方形边长为1.
(1)已知△ABC的顶点都在格点上,请直接写出△ABC的面积S= ;
(2)请以点O为位似中心,相似比为2,在方格纸中将△ABC放大,画出放大后的图形△A′B'C';
(3)求△A′B'C′的面积S′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的内切圆,切点分别相为点D、E、F,设△ABC的面积、周长分别为S、l,⊙O的半径为r,则下列等式:
①∠AED+∠BFE+∠CDF=180°;②S=![]() l r;③2∠EDF=∠A+∠C;④2(AD+CF+BE)=l,其中成立的是( )
l r;③2∠EDF=∠A+∠C;④2(AD+CF+BE)=l,其中成立的是( )
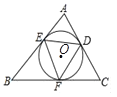
A.①②③④B.②③④C.①③④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.下列叙述正确的是( )

A. 小球的飞行高度不能达到15m
B. 小球的飞行高度可以达到25m
C. 小球从飞出到落地要用时4s
D. 小球飞出1s时的飞行高度为10m
查看答案和解析>>
科目:初中数学 来源: 题型:
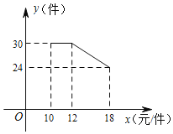
【题目】 某网店销售一种产品.这种产品的成本价为10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/件市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示:
(1)当12≤x≤18时,求y与x之间的函数关系式;
(2)求每天的销售利润w(元)与销售价x(元/件)之间的函数关系式并求出每件销售价为多少元时.每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究函数![]() 的图象与性质.
的图象与性质.
(1)下表是y与x的几组对应值.
| … |
|
|
|
|
|
|
| … |
| … |
|
|
|
|
|
|
| … |
其中m的值为_______________;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并已画出了函数图象的一部分,请你画出该图象的另一部分;
(3)结合函数的图象,写出该函数的一条性质:_____________________________;
(4)若关于x的方程![]() 有2个实数根,则t的取值范围是___________________.
有2个实数根,则t的取值范围是___________________.
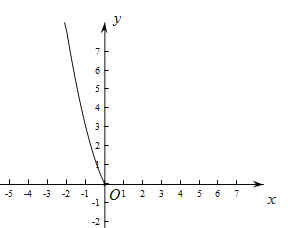
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学在一次用频率估计概率的试验中,统计了某一结果出现的频率,给出的 统计图如图所示,则符合这一结果的试验可能是 ( )
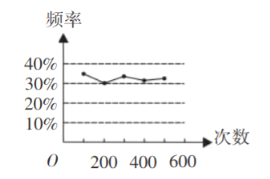
A.掷一枚硬币,出现正面朝上的概率
B.掷一枚硬币,出现反面朝上的概率
C.掷一枚骰子,出现 ![]() 点的概率
点的概率
D.从只有颜色不同的两个红球和一个黄球中,随机取出一个球是黄球的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1) 若确定甲打第一场,再从其余三位同学中随机选取一位,恰好选中乙同学的概率是 .
(2) 若随机抽取两位同学,请用画树状图法或列表法,求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com