
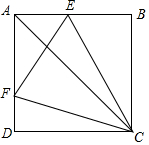
 如图,E,F分别是边长为a的正方形ABCD的边AB,AD上的点,∠ECF=45°.
如图,E,F分别是边长为a的正方形ABCD的边AB,AD上的点,∠ECF=45°.分析 (1)如图1中,延长AD到G,使DG=BE.只要证明△ECF≌△GCF即可解决问题.
(2)如图2中,过E作EP⊥AC,垂足为P.由△ECP≌△FCD,可得$\frac{CE}{CF}$=$\frac{CP}{CD}$,设CD=BC=AB=a,AC=$\sqrt{2}$a,∠EAP=45°,推出AP=$\frac{\sqrt{2}}{2}$AE,BC=$\frac{\sqrt{2}}{2}$AC,可得$\frac{CE}{CF}$=$\frac{CP}{CD}$=$\frac{AC-AP}{AB}$=$\frac{AC-\frac{\sqrt{2}}{2}AE}{\frac{\sqrt{2}}{2}AC}$=$\sqrt{2}$-$\frac{AE}{AC}$=$\sqrt{2}$-$\frac{AE}{\sqrt{2}AB}$=$\sqrt{2}$-$\frac{\sqrt{2}}{2}$k;
(3)①解法一:在Rt△AEF中根据勾股定理得:[4-(x+y)]2=x2+y2,进行变形即可;
解法二:由$\frac{AE}{AB}$=$\frac{x}{2}$,$\frac{AF}{AD}$=$\frac{y}{2}$,由(2)得:$\frac{CE}{CF}$=$\sqrt{2}$-$\frac{\sqrt{2}}{2}$k=$\sqrt{2}$-$\frac{\sqrt{2}}{4}$x,同理可得$\frac{CF}{CE}$=$\sqrt{2}$-$\frac{\sqrt{2}}{4}$y,由$\frac{CE}{CF}$•$\frac{CF}{CE}$=1,可得($\sqrt{2}$-$\frac{\sqrt{2}}{4}$x)($\sqrt{2}$-$\frac{\sqrt{2}}{4}$y)=1,由此即可解决问题;
②根据条件把问题转化为不等式组解决;
解答 解:(1)证明:延长AD到G,使DG=BE.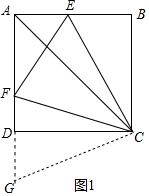
∵四边形ABCD是正方形,
∴BC=DC,∠B=∠ADC=90°,
∴∠CDG=∠B=90°,
∴△CBE≌△CDG,
∴∠BCE=∠DCG,CE=CG,
∴∠DCG+∠ECD=∠BCE+∠ECD=90°,
∵∠ECF=45°,
∴∠GCF=∠ECF=45°,
又∵CE=CG,CF=CF,
∴△ECF≌△GCF,
∴∠CFE=∠CFG,即CF平分∠DFE.
(2)如图2,过E作EP⊥AC,垂足为P.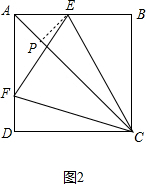
∵∠ECF+∠ACF=∠FCD+∠ACF=45°,
∴∠ECF=45°-∠ACF=∠FCD,
又∵∠EPC=∠FDC=90°,
∴△ECP≌△FCD,
∴$\frac{CE}{CF}$=$\frac{CP}{CD}$,
∵四边形ABCD是正方形,
∴CD=BC=AB=a,AC=$\sqrt{2}$a,∠EAP=45°,
∴AP=$\frac{\sqrt{2}}{2}$AE,BC=$\frac{\sqrt{2}}{2}$AC,
∴$\frac{CE}{CF}$=$\frac{CP}{CD}$=$\frac{AC-AP}{AB}$=$\frac{AC-\frac{\sqrt{2}}{2}AE}{\frac{\sqrt{2}}{2}AC}$=$\sqrt{2}$-$\frac{AE}{AC}$=$\sqrt{2}$-$\frac{AE}{\sqrt{2}AB}$=$\sqrt{2}$-$\frac{\sqrt{2}}{2}$k,
(3)①解法1:如图1,由(1)知,△ECF≌△GCF,BE=2-x,DF=2-y,
∴EF=GF=4-(x+y)
在Rt△AEF中根据勾股定理得:[4-(x+y)]2=x2+y2,
整理,得:xy-4(x+y)+8=0,(x-4)(y-4)=8,y-4=$\frac{8}{x-4}$,
所以y与x之间的函数解析式为y=4+$\frac{8}{x-4}$,x的取值范围是0≤x≤2.
解法2:∵$\frac{AE}{AB}$=$\frac{x}{2}$,$\frac{AF}{AD}$=$\frac{y}{2}$,由(2)得:$\frac{CE}{CF}$=$\sqrt{2}$-$\frac{\sqrt{2}}{2}$k=$\sqrt{2}$-$\frac{\sqrt{2}}{4}$x,
同理可得$\frac{CF}{CE}$=$\sqrt{2}$-$\frac{\sqrt{2}}{4}$y,
∵$\frac{CE}{CF}$•$\frac{CF}{CE}$=1,
∴($\sqrt{2}$-$\frac{\sqrt{2}}{4}$x)($\sqrt{2}$-$\frac{\sqrt{2}}{4}$y)=1,
∴(1-$\frac{1}{4}$x)(1-$\frac{1}{4}$y)=$\frac{1}{2}$;
(x-4)(y-4)=8,即y=4+$\frac{8}{x-4}$,x的取值范围是0≤x≤2.
②∵$\frac{CE}{CF}$=$\sqrt{2}$-$\frac{\sqrt{2}}{4}$x,$\frac{5\sqrt{2}}{8}$≤$\frac{CE}{CF}$≤$\frac{3\sqrt{2}}{4}$,
∴$\left\{\begin{array}{l}{\sqrt{2}-\frac{\sqrt{2}}{4}x≥\frac{5\sqrt{2}}{8}}\\{\sqrt{2}-\frac{\sqrt{2}}{4}x≤\frac{3\sqrt{2}}{4}}\end{array}\right.$,解这个不等式组,得:1≤x≤$\frac{3}{2}$;
画出函数y=4+$\frac{8}{x-4}$的图象如图3:
由图象可知:当1≤x≤$\frac{3}{2}$时,y随x的增大而减小,
当x=1时,y=$\frac{4}{3}$,
当x=$\frac{3}{2}$时,y=$\frac{12}{7}$,
所以y的取值范围是$\frac{4}{3}$≤y≤$\frac{12}{7}$.
点评 本题考查相似形综合题、正方形的性质、全等三角形的判定和性质、勾股定理、不等式组等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数解决问题,属于中考压轴题.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
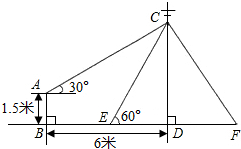 如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
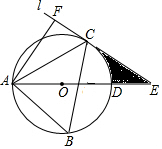 如图,△ABC内接于⊙O,且∠B=60°,过C作⊙O的切线l,与直径AD的延长线交于点E,AF⊥l,垂足为F.
如图,△ABC内接于⊙O,且∠B=60°,过C作⊙O的切线l,与直径AD的延长线交于点E,AF⊥l,垂足为F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com