
| x (万元) | … | 50 | 60 | 70 | 80 | … |
| P(万元) | … | 40 | 41 | 40 | 37 | … |
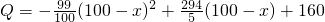 (万元).
(万元).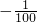 a+120,成本为20元/件;国外销售情况为:价格为120元/件,国外销售成本为40元/件.该集团要将8000件产品全部销售完并获得312000元的利润,该集团该怎样安排国内的销售量?(精确到个位)
a+120,成本为20元/件;国外销售情况为:价格为120元/件,国外销售成本为40元/件.该集团要将8000件产品全部销售完并获得312000元的利润,该集团该怎样安排国内的销售量?(精确到个位)

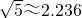 )
)  ,
, ,
,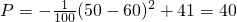 (万元),
(万元), ,
, a+120-20)a+80(8000-a)=312000,
a+120-20)a+80(8000-a)=312000, (舍),
(舍), ,整理求解即可求得最大值,则可求得5年所获利润的最大值;
,整理求解即可求得最大值,则可求得5年所获利润的最大值;

科目:初中数学 来源: 题型:阅读理解
重庆西永微电园入驻企业----方正集团开发了一种新型电子产品,是未来五年IT行业倍受青睐的产品.在五年销售期限内,方正集团每年对该产品最多可投入100万元销售投资,该集团营销部门根据市场分析,对该产品的销售投资收益拟定了两种销售方案:
方案一:只在国内销售,每投入![]() 万元,每年可获得利润P与x关系如下表所示:
万元,每年可获得利润P与x关系如下表所示:
| x (万元) | … | 50 | 60 | 70 | 80 | … |
| P(万元) | … | 40 | 41 | 40 | 37 | … |
方案二:五年销售期限内,每年均投入100万元销售投资。前两年中,每年拨出50万元用于筹备国际营销平台,两年筹备完成, 完成前该产品只能在国内销售;国际营销平台完成后的3年中,该产品既在国内销售,也在国外销售,在国内销售的投资收益仍满足方案一,而在国外销售的投资收益为:每年投入![]() 万元,可获年利润
万元,可获年利润![]() (万元).
(万元).
1.请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出P与x之间的函数关系式,并求出选择方案一该集团每年所获利润的最大值.
2.若选择方案二,设后3年中每年用于国内销售的投入为n(万元),则n为何值时可使这5年所获总利润(扣除筹备国际营销平台资金后)最大?并求出该最大值.
3.方正集团的国际营销平台也可销售该集团其它产品,方正集团决定将另一种产品也销往国外.已知,该产品在国内销售情况为:售价y(元/件)与销量a(件)的函数关系式为y=![]() a+120,成本为20元/件;国外销售情况为:价格为120元/件,国外销售成本为40元/件.该集团要将8000件产品全部销售完并获得312000元的利润,该集团该怎样安排国内的销售量?(精确到个位)
a+120,成本为20元/件;国外销售情况为:价格为120元/件,国外销售成本为40元/件.该集团要将8000件产品全部销售完并获得312000元的利润,该集团该怎样安排国内的销售量?(精确到个位)
(参考数据: ![]()
![]()
![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 万元,每年可获得利润P与x关系如下表所示:
万元,每年可获得利润P与x关系如下表所示:| x (万元) | … | 50 | 60 | 70 | 80 | … |
| P(万元) | … | 40 | 41 | 40 | 37 | … |
 万元,可获年利润
万元,可获年利润 (万元).
(万元). a+120,成本为20元/件;国外销售情况为:价格为120元/件,国外销售成本为40元/件.该集团要将8000件产品全部销售完并获得312000元的利润,该集团该怎样安排国内的销售量?(精确到个位)
a+120,成本为20元/件;国外销售情况为:价格为120元/件,国外销售成本为40元/件.该集团要将8000件产品全部销售完并获得312000元的利润,该集团该怎样安排国内的销售量?(精确到个位) 

 )
)查看答案和解析>>
科目:初中数学 来源:2011-2012学年重庆市九年级3月月考数学试卷(解析版) 题型:解答题
重庆西永微电园入驻企业----方正集团开发了一种新型电子产品,是未来五年IT行业倍受青睐的产品.在五年销售期限内,方正集团每年对该产品最多可投入100万元销售投资,该集团营销部门根据市场分析,对该产品的销售投资收益拟定了两种销售方案:
方案一:只在国内销售,每投入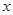 万元,每年可获得利润P与x关系如下表所示:
万元,每年可获得利润P与x关系如下表所示:
|
x (万元) |
… |
50 |
60 |
70 |
80 |
… |
|
P(万元) |
… |
40 |
41 |
40 |
37 |
… |
方案二:五年销售期限内,每年均投入100万元销售投资。前两年中,每年拨出50万元用于筹备国际营销平台,两年筹备完成, 完成前该产品只能在国内销售;国际营销平台完成后的3年中,该产品既在国内销售,也在国外销售,在国内销售的投资收益仍满足方案一,而在国外销售的投资收益为:每年投入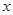 万元,可获年利润
万元,可获年利润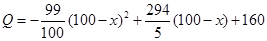 (万元).
(万元).
1.请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出P与x之间的函数关系式,并求出选择方案一该集团每年所获利润的最大值.
2.若选择方案二,设后3年中每年用于国内销售的投入为n(万元),则n为何值时可使这5年所获总利润(扣除筹备国际营销平台资金后)最大?并求出该最大值.
3.方正集团的国际营销平台也可销售该集团其它产品,方正集团决定将另一种产品也销往国外.已知,该产品在国内销售情况为:售价y(元/件)与销量a(件)的函数关系式为y
=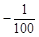 a+120,成本为20元/件;国外销售情况为:价格为120元/件,国外销售成本为40元/件.该集团要将8000件产品全部销售完并获得312000元的利润,该集团该怎样安排国内的销售量?(精确到个位)
a+120,成本为20元/件;国外销售情况为:价格为120元/件,国外销售成本为40元/件.该集团要将8000件产品全部销售完并获得312000元的利润,该集团该怎样安排国内的销售量?(精确到个位)
(参考数据: 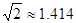
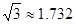
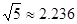 )
)
查看答案和解析>>
科目:初中数学 来源:2012届重庆市重庆一中九年级3月月考数学试卷(带解析) 题型:解答题
重庆西永微电园入驻企业----方正集团开发了一种新型电子产品,是未来五年IT行业倍受青睐的产品.在五年销售期限内,方正集团每年对该产品最多可投入100万元销售投资,该集团营销部门根据市场分析,对该产品的销售投资收益拟定了两种销售方案:
方案一:只在国内销售,每投入 万元,每年可获得利润P与x关系如下表所示:
万元,每年可获得利润P与x关系如下表所示:
| x (万元) | … | 50 | 60 | 70 | 80 | … |
| P(万元) | … | 40 | 41 | 40 | 37 | … |
 万元,可获年利润
万元,可获年利润 (万元).
(万元). a+120,成本为20元/件;国外销售情况为:价格为120元/件,国外销售成本为40元/件.该集团要将8000件产品全部销售完并获得312000元的利润,该集团该怎样安排国内的销售量?(精确到个位)
a+120,成本为20元/件;国外销售情况为:价格为120元/件,国外销售成本为40元/件.该集团要将8000件产品全部销售完并获得312000元的利润,该集团该怎样安排国内的销售量?(精确到个位) 

 )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com