
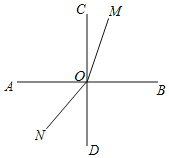
【题目】如图,两条直线AB,CD相交于点O,且![]() ,射线OM从OB开始绕O点逆时针方向旋转,速度为
,射线OM从OB开始绕O点逆时针方向旋转,速度为![]() ,射线ON同时从OD开始绕O点顺时针方向旋转,速度为
,射线ON同时从OD开始绕O点顺时针方向旋转,速度为![]() .两条射线OM、ON同时运动,运动时间为t秒.(本题出现的角均小于平角)
.两条射线OM、ON同时运动,运动时间为t秒.(本题出现的角均小于平角)
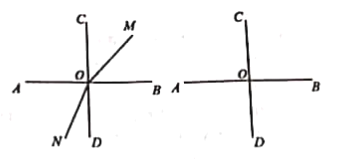
(1)当![]() 时,若
时,若![]() .试求出的值;
.试求出的值;
(2)当![]() 时,探究
时,探究![]() 的值,问:t满足怎样的条件是定值;满足怎样的条件不是定值?
的值,问:t满足怎样的条件是定值;满足怎样的条件不是定值?
【答案】(1)t的值为1秒或![]() 秒;
秒;
(2)当0<t<![]() 时,
时,![]() 的值是1;当
的值是1;当![]() <t<6时,
<t<6时,![]() 不是定值.
不是定值.
【解析】
(1)分两种情况:①如图所示,当0<t≤7.5时,②如图所示,当7.5<t<12时,分别根据已知条件列等式可得t的值;
(2)分两种情况,分别计算∠COM、∠BON和∠MON的度数,代入可得结论.
(1)当ON与OA重合时,t=90÷12=7.5(s)
当OM与OA重合时,t=180°÷15=12(s)
①如图所示,当0<t≤7.5时,∠AON=90°-12t°,∠AOM=180°-15t°,
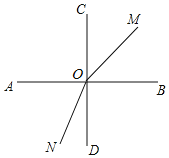
由∠AOM=3∠AON-69°,可得180-15t=3(90-12t)-69,
解得t=1;
②如图所示,当7.5<t<12时,∠AON=12t°-90°,∠AOM=180°-15t°,
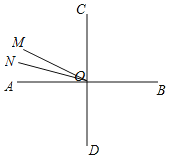
由∠AOM=3∠AON-69°,可得180-15t=3(12t-90)-69,解得t=![]() ,
,
综上,t的值为1秒或![]() 秒;
秒;
(2)当∠MON=180°时,∠BOM+∠BOD+∠DON=180°,
∴15t+90+12t=180,解得t=![]() ,
,
①如图所示,当0<t<![]() 时,∠COM=90°-15t°,∠BON=90°+12t°,
时,∠COM=90°-15t°,∠BON=90°+12t°,
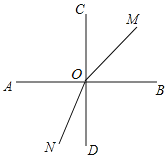
∠MON=∠BOM+∠BOD+∠DON=15t°+90°+12t°=![]() ,
,
∴![]() =
=![]() =
=![]() =1(是定值),
=1(是定值),
②如图所示,当![]() <t<6时,∠COM=90°-15t°,∠BON=90°+12t°,
<t<6时,∠COM=90°-15t°,∠BON=90°+12t°,
∠MON=360°-/span>(∠BOM+∠BOD+∠DON)=360°-(15t°+90°+12t°)=270°-27t°,
∴![]() =
=![]() =
=![]() (不是定值),
(不是定值),
综上所述,当0<t<![]() 时,
时,![]() 的值是1;当
的值是1;当![]() <t<6时,
<t<6时,![]() 不是定值.
不是定值.


科目:初中数学 来源: 题型:
【题目】在有些情况下,不需要计算出结果也能把绝对值符号去掉.例如:|6+7|=6+7;|6﹣7|=7﹣6;|7﹣6|=7﹣6;|﹣6﹣7|=6+7
(1)根据上面的规律,把下列各式写成去掉绝对值符号的形式:
①|7﹣21|= ;②|﹣![]() ﹣0.8|= ;③|
﹣0.8|= ;③|![]() ﹣
﹣![]() |= :
|= :
(2)数a在数轴上的位置如图所示,则|a﹣2.5|= .
![]()
A.a﹣2.5
B.2.5﹣a
C.a+2.5
D.﹣a﹣2.5
(3)利用上述介绍的方法计算或化简:
①|![]() ﹣
﹣![]() |+|
|+|![]() ﹣
﹣![]() |﹣|﹣
|﹣|﹣![]() |+
|+![]() ;
;
②|![]() ﹣
﹣![]() |+|
|+|![]() ﹣
﹣![]() |﹣|﹣
|﹣|﹣![]() |+2(
|+2(![]() ),其中a>2.
),其中a>2.
查看答案和解析>>
科目:初中数学 来源: 题型:
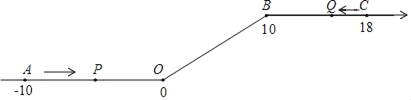
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位,动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半;点P从点A出发的同时,点Q从点C出发,以1单位/秒的速度沿着“折线数轴”的负方向运动,当点P到达B点时,点P、Q均停止运动.设运动的时间为t秒.问:
(1)用含t的代数式表示动点P在运动过程中距O点的距离;
(2)P、Q两点相遇时,求出相遇时间及相遇点M所对应的数是多少?
(3)是否存在P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等时?若存在,请直接写出t的取值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青岛交运集团出租车司机张师傅某天下午的营运全是在东西走向的吉林路上进行的,如果规定向东为正,向西为负,他这天下午行车里程![]() 单位:千米
单位:千米![]() 如下:
如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)张师傅这天最后到达目的地时,在下午出车时的出发地哪个方向?距离出发地多远?
(2)张师傅这天下午共行车多少千米?
(3)若每千米耗油![]() ,则这天下午张师傅用了多少升油?
,则这天下午张师傅用了多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
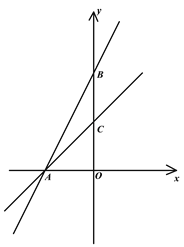
【题目】如图,在平面直角坐标系中,直线AB:y=kx+4(k≠0)与x轴,y轴,交于A、B两点,点C是BO的中点且tan∠ABO=![]()
(1)求直线AC的解析式;
(2)若点M是直线AC的一点,当![]() 时,求点M的坐标.
时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个一次函数的图像与![]() 轴交于同一点,则称这两个函数为一对“
轴交于同一点,则称这两个函数为一对“![]() 牵手函数”,这个交点为“
牵手函数”,这个交点为“![]() 牵手点”.
牵手点”.
(1)一次函数![]() 与
与![]() 轴的交点坐标为________;一次函数
轴的交点坐标为________;一次函数![]() 与一次函数
与一次函数![]() 为一对“
为一对“![]() 牵手函数”,则
牵手函数”,则![]() ________;
________;
(2)请写出以![]() 为“
为“![]() 牵手点”的一对“
牵手点”的一对“![]() 牵手函数”;
牵手函数”;
(3)已知一对“![]() 牵手函数”:
牵手函数”:![]() 与
与![]() ,其中
,其中![]() ,
,![]() 为一元二次方程
为一元二次方程![]() 的两根,求它们的“
的两根,求它们的“![]() 牵手点”.
牵手点”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知ab<0,![]() ,且|c|>|b|>|a|,数轴上a、b、c对应的点是A、B、C.
,且|c|>|b|>|a|,数轴上a、b、c对应的点是A、B、C.
(1) 若|a|=-a时,请在数轴上标出A、B、C的大致位置;
(2) 在(1)的条件下,化简:|a-b|-|b+c|+|c+a|.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
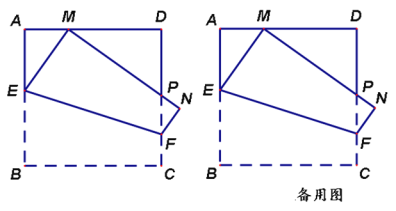
【题目】如图,在边长为1的正方形ABCD中,动点E,F分别在边AB,CD上,将正方形ABCD沿直线EF折叠,使点B的对应点M始终落在边AD上(点M不与点A,D重合),点C落在点N处,MN与CD交于点P,设BE=x。
(1)当AM=![]() 时,求x的值;
时,求x的值;
(2)随着点M在边AD上位置的变化,ΔPDM的周长是否发生变化?如变化,请说明理由;如不变,请求出该定值;
(3)若AM=a,四边形BEFC的面积为S,求S与a之间的函数表达式。
查看答案和解析>>
科目:初中数学 来源: 题型:
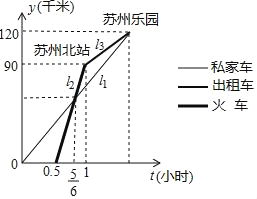
【题目】“五一”期间小明和小丽相约到苏州乐园游玩,小丽乘私家车从上海出发30分钟后,小明乘坐火车从上海出发,先到苏州北站,然后再乘出租车去游乐园(换乘时间忽略不计),两人恰好同时到达苏州乐园,他们离上海的距离y(千米)与乘车时间t(小时)的关系如图所示,请结合图象信息解决下面问题:
(1)本次火车的平均速度_________千米/小时?
(2)当小明到达苏州北站时,小丽离苏州乐园的距离还有多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com