
分析 根据标志符的定义,代入数据即可求出[A]的值,结合点M的坐标以及[M]=3,即可得出[M]=|m+1|+|m2-4m|=3,分m<-1、-1≤m<0、0≤m≤4和m>4四种情况去掉绝对值符号,解一元二次方程求出m值,将其代入点M的坐标即可得出结论.
解答 解:∵我们规定[P]=|x|+|y|,[P]为点P(x,y)的标志符,
∴[A]=|-3|+|2|=5,
故答案为:5.
∵点M(m+1,m2-4m)的标志符为[M]=3,
∴[M]=|m+1|+|m2-4m|=3.
当m<-1时,有-m-1+m2-4m=3,即m2-5m-4=0,
解得:m1=$\frac{5-\sqrt{41}}{2}$(舍去),m2=$\frac{5+\sqrt{41}}{2}$(舍去);
当-1≤m<0时,有m+1+m2-4m=3,即m2-3m-2=0,
解得:m3=$\frac{3-\sqrt{17}}{2}$,m4=$\frac{3+\sqrt{17}}{2}$(舍去),
此时点M的坐标为($\frac{5-\sqrt{17}}{2}$,$\frac{1+\sqrt{17}}{2}$);
当0≤m≤4时,有m+1-m2+4m=3,即m2-5m+2=0,
解得:m5=$\frac{5-\sqrt{17}}{2}$,m6=$\frac{5+\sqrt{17}}{2}$(舍去),
此时点M的坐标为($\frac{7-\sqrt{17}}{2}$,$\frac{1-2\sqrt{17}}{4}$);
当m>4时,有m+1+m2-4m=3,即m2-3m-2=0,
解得:m3=$\frac{3-\sqrt{17}}{2}$(舍去),m4=$\frac{3+\sqrt{17}}{2}$(舍去).
综上所述:符合条件的点M的坐标为($\frac{5-\sqrt{17}}{2}$,$\frac{1+\sqrt{17}}{2}$)或($\frac{7-\sqrt{17}}{2}$,$\frac{1-2\sqrt{17}}{4}$).
点评 本题考查了坐标与图形的性质、含绝对值符合的一元二次方程以及公式法解一元二次方程,熟读题干,明白标志符的概念,并能运用[P]=|x|+|y|解决问题是解题的关键.


科目:初中数学 来源: 题型:解答题
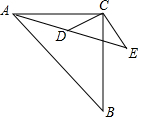 如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AE上,若AC=10,AD=2$\sqrt{10}$,求DC的长.
如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AE上,若AC=10,AD=2$\sqrt{10}$,求DC的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
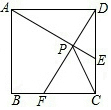 如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=2,线段CP的最小值是( )
如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=2,线段CP的最小值是( )| A. | $\sqrt{2}$ | B. | $\sqrt{5}$-1 | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
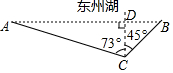 某市为了创建绿色生态城市,在城东建了“东州湖”景区,小明和小亮想测量“东州湖”东西两端A、B间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点B的一点C,并测得BC=350米,点A位于点C的北偏西73°方向,点B位于点C的北偏东45°方向.
某市为了创建绿色生态城市,在城东建了“东州湖”景区,小明和小亮想测量“东州湖”东西两端A、B间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点B的一点C,并测得BC=350米,点A位于点C的北偏西73°方向,点B位于点C的北偏东45°方向.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com