
【题目】抛物线y=ax2+bx+c上部分点的横坐标x和纵坐标y的对应值如下表,则下列说法中正确的有_______.(填序号)
x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
y | … | -37 | -21 | -9 | -1 | 3 | 3 | … |
①当x>1时,y随x的增大而减小. ②抛物线的对称轴为直线x=-![]() .
.
③当x=2时,y=-9. ④方程ax2+bx+c=0一个正数解![]() 满足1<
满足1<![]() <2.
<2.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
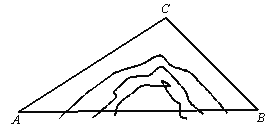
【题目】如图,A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道,建成A,B两地的直达高铁,可以缩短从A地到B地的路程.已知:∠CAB=30°,∠CBA=45°,AC=580公里,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少公里?(参考数据:![]() 1.7,
1.7,![]() 1.4)
1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
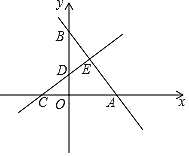
【题目】如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A、点B,直线CD与x轴、y轴分别交于点C、点D,AB与CD相交于点E,线段OA、OC的长是一元二次方程x2﹣18x+72=0的两根(OA>OC),BE=5,OB=![]() OA.
OA.
(1)求点A、点C的坐标;
(2)求直线CD的解析式;
(3)在x轴上是否存在点P,使点C、点E、点P为顶点的三角形与△DCO相似?若存在,请求出点P的坐标;如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(﹣3,4),B(﹣4,2),C(﹣2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1,将△A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2.
(1)画出△A1B1C1和△A2B2C2;
(2)△ABC经旋转、平移后点A的对应点分别为A1、A2,请写出点A1、A2的坐标;
(3)P(a,b)是△ABC的边AC上一点,△ABC经旋转、平移后点P的对应点分别为P1,P2,请写出点P1、P2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
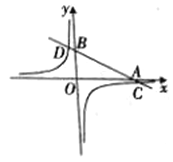
【题目】如图,在平面直角坐标系中,一次函数y= kx +b(k≠0)的图象分别交x轴、y轴于A、B两点,与反比例函数y=![]() (m≠0)的图象交于C、D两点。已知点C的坐标是(6,-1),D(n,3).
(m≠0)的图象交于C、D两点。已知点C的坐标是(6,-1),D(n,3).
(1)求m的值和点D的坐标;
(2)求线段AB的长度;
(3)根据图象直接写出: 当x为何值时,一次函数的值大于反比例函数的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在课外学习时遇到这样一个问题:
定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2
(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.求y=-2x2+5x-3函数的“旋转函数”.
小明是这样思考的:由y=-2x2+5x-3函数可知,a1=-2,b1=5,c1=-3,根据a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2就能确定这个函数的“旋转函数”.
请参考小明的方法解决下面的问题:
(1)写出函数y=-2x2+5x-3的“旋转函数”;
(2)若函数y1=x2+![]() x-n与y2=-x2-mx-2互为“旋转函数”,求(m+n)2019的值;
x-n与y2=-x2-mx-2互为“旋转函数”,求(m+n)2019的值;
(3)已知函数y=![]() (x-2)(x+3)的图像与
(x-2)(x+3)的图像与![]() 轴交于A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1、B1、C1,试证明经过点A1、B1、C1的二次函数与函数y=
轴交于A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1、B1、C1,试证明经过点A1、B1、C1的二次函数与函数y=![]() (x-2)(x+3)互为“旋转函数”.
(x-2)(x+3)互为“旋转函数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 与双曲线
与双曲线![]() 的一个交点是
的一个交点是![]() .
.
(1)求![]() 的值;
的值;
(2)设点![]() 是双曲线
是双曲线![]() 上不同于
上不同于![]() 的一点,直线
的一点,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
①若![]() ,求
,求![]() 的值;
的值;
②若![]() ,结合图象,直接写出
,结合图象,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店参加某校读书活动,并为每班准备了A,B两套名著,赠予各班甲、乙两名优秀读者,以资鼓励.某班决定采用游戏方式发放,其规则如下:将三张除了数字2,5,6不同外其余均相同的扑克牌,数字朝下随机平铺于桌面,从中任取2张,若牌面数字之和为偶数,则甲获A名著;若牌面数字之和为奇数,则乙获得A名著,你认为此规则合理吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如下图)
你选择的方案是_____(填方案一,方案二,或方案三),则B点坐标是______,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com