
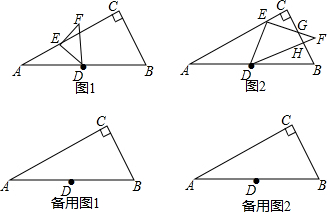
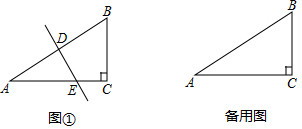
���� ��1������ֱ��������30�Ƚ��������BC�������ù��ɶ������AC���ɣ�
��2������ͼ1�У���DM��AC��M����Rt��ADM�����DM��AM����֤����DEM�ǵ���ֱ�������μ��ɽ�����⣮
����ͼ2�У�����S�ı���DEGH=S��DEF-S��GHF���㼴�ɽ�����⣮
��3�����������Σ�����ͼ3�У�����F��BC����ʱ������ͼ4�У�����F��BC����ʱ����DM��AC��M������ͼ5�У�����F��AB���ӳ�����ʱ����EM��AB��M����BM=x������ͼ6�У�����F��CB���ӳ�����ʱ���ֱ������E���˶�·�̣����ɽ�����⣮
��� �⣺��1����Rt��ABC�У��ߡ�C=90�㣬��A=30�㣬AB=12��
��BC=$\frac{1}{2}$AB=6��AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$��
�ʴ�Ϊ6$\sqrt{3}$��6��
��2������ͼ1�У���DM��AC��M��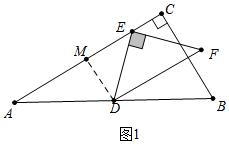
�ߡ�DEF�ǵ���ֱ�������Σ�
���EDF=45�㣬
��AC��DF��
���AED=��EDF=45�㣬
���EDM=90��-��AED=45�㣬
���NED=��MDE=45�㣬
��DM=ME��
��AD=DB=6����A=30�㣬��AMD=90�㣬
��DM=ME=3��AM=$\sqrt{A{D}^{2}-D{M}^{2}}$=3$\sqrt{3}$��
��AE=3$\sqrt{3}$+3��
��t=��3+3$\sqrt{3}$��s��
����ͼ2�У�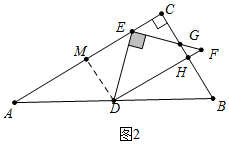
�ɢٿ�֪��DE=F=3$\sqrt{2}$��EC=AC-AE=6$\sqrt{3}$-��3+3$\sqrt{3}$��=3$\sqrt{3}$-3��
�ߡ�DMC=��C=��MDH=90�㣬
���ı���DMCH�Ǿ��Σ�
��CH=DM=3��
�ߡ�CEG=��CGE=45�㣬
��EC=CG=3$\sqrt{3}$-3��
�ߡ�F=��HGF=45�㣬
��HF=HG=3-��3$\sqrt{3}$-3��=6-3$\sqrt{3}$��
��S�ı���DEGH=S��DEF-S��GHF=$\frac{1}{2}$����3$\sqrt{2}$��2-$\frac{1}{2}$��6-3$\sqrt{3}$��2=18$\sqrt{3}$-$\frac{45}{2}$��
�ʴ�Ϊ18$\sqrt{3}$-$\frac{45}{2}$��
��3������ͼ3�У�����F��BC����ʱ����Rt��AED�У��ߡ�AED=90�㣬��A=30�㣮AD=6��
��DE=3��AE=3$\sqrt{3}$��
��t=3$\sqrt{3}$��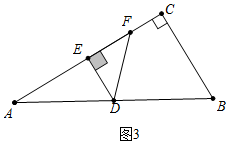
����ͼ4�У�����F��BC����ʱ����DM��AC��M��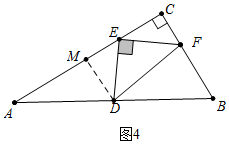
�ߡ�MED+��MDE=90�㣬��MED+��CEF=90�㣬
���CEF=��MDE����DE=EF����DME=��C=90�㣬
���DME�ա�ECF��
��DM=CE=3��
��AE=AC=CE=6$\sqrt{3}$-3��
��t=6$\sqrt{3}$-3��
����ͼ5�У�����F��AB���ӳ�����ʱ����EM��AB��M����BM=x��
��Rt��EMB�У��ߡ�EMB=90�㣬��MEB=30�㣬BM=x��
��EB=2x��EM=$\sqrt{3}$x��
��Rt��DEM�У��ߡ�EDM=��DEM=45�㣬
��DM=EM=$\sqrt{3}$x��
��DB=6��
��$\sqrt{3}$x+x=6��
��x=3��$\sqrt{3}$-1����
��BE=6��$\sqrt{3}$-1����
��AC+CE=6$\sqrt{3}$+6-6��$\sqrt{3}$-1��=12��
t=12��
����ͼ6�У�����F��CB���ӳ�����ʱ����֪CE=EB=3��AC+CE=6$\sqrt{3}$+3��
��t=6$\sqrt{3}$+3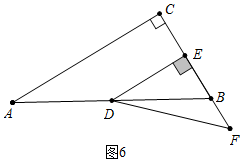
������������t=3$\sqrt{3}$s��6$\sqrt{3}$-3��s��12s��6$\sqrt{3}$+3��sʱ����F�ڡ�ABC�������ڵ�ֱ���ϣ�
���� ���⿼���������ۺ��⡢ȫ�������ε��ж������ʡ����ɶ���������ֱ�������ε����ʡ�30�ȵ�ֱ�������ε����ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ��������ۣ�ע�ⲻ��©�⣮�����п�ѹ���⣮


 �����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д� Сѧ�����ҵ���ϴ�ѧ������ϵ�д�
Сѧ�����ҵ���ϴ�ѧ������ϵ�д� ���Ž�����ٰθ��νӹ㶫���������ϵ�д�
���Ž�����ٰθ��νӹ㶫���������ϵ�д� �����������ҵ�������������ϵ�д�
�����������ҵ�������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
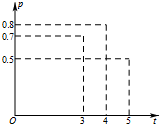 �ӹ�����ʱ�������Ҳ����������İٷֱȳ�Ϊ����ʳ���ʡ������ض������£���ʳ����p��ӹ�ʱ��t����λ�����ӣ�����ĺ�����ϵp=at2+bt+c��a��b��c�dz���������ͼ��¼������ʵ������ݣ�������������ģ�ͺ�ʵ�����ݣ����Եõ���Ѽӹ�ʱ��Ϊ��������
�ӹ�����ʱ�������Ҳ����������İٷֱȳ�Ϊ����ʳ���ʡ������ض������£���ʳ����p��ӹ�ʱ��t����λ�����ӣ�����ĺ�����ϵp=at2+bt+c��a��b��c�dz���������ͼ��¼������ʵ������ݣ�������������ģ�ͺ�ʵ�����ݣ����Եõ���Ѽӹ�ʱ��Ϊ��������| A�� | 3.50���� | B�� | 3.75���� | C�� | 4.00���� | D�� | 4.25���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
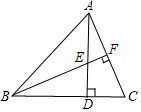 ��ͼ��AD�ǡ�ABCһ���ϵĸߣ�BF��AC��BE=AC��
��ͼ��AD�ǡ�ABCһ���ϵĸߣ�BF��AC��BE=AC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
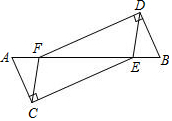 ��ͼ��A��F��E��B�ĵ㹲�ߣ�AC��CE��BD��DF��AE=BF��AC=BD����֤��CF��DE��
��ͼ��A��F��E��B�ĵ㹲�ߣ�AC��CE��BD��DF��AE=BF��AC=BD����֤��CF��DE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3a+2b=5ab | B�� | 7ab-4ba=0 | C�� | 4x2y-3xy2=x2y | D�� | 3x2+5x2=8x2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com