
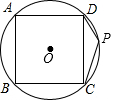
 如图,正方形ABCD的四个顶点分别在⊙O上,点P在$\widehat{CD}$上不同于点C的任意一点,则∠DPC的度数是135度.
如图,正方形ABCD的四个顶点分别在⊙O上,点P在$\widehat{CD}$上不同于点C的任意一点,则∠DPC的度数是135度.  小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:选择题
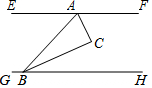 如图,Rt△ABC的锐角顶点A、B分别在直线EF、GH上,且EF∥GH,若∠CAF=65°,则∠CBH的度数为( )
如图,Rt△ABC的锐角顶点A、B分别在直线EF、GH上,且EF∥GH,若∠CAF=65°,则∠CBH的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
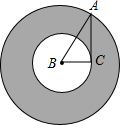 如图,在Rt△ABC中,∠ACB=90°,AC=$\sqrt{2}$,将其绕B点顺时针旋转一周,则分别以BA、BC为半径的圆形成一个圆环,则该圆环的面积为( )
如图,在Rt△ABC中,∠ACB=90°,AC=$\sqrt{2}$,将其绕B点顺时针旋转一周,则分别以BA、BC为半径的圆形成一个圆环,则该圆环的面积为( )| A. | $\sqrt{2}π$ | B. | 2π | C. | 4π | D. | 6π |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
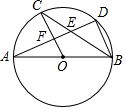 如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②CB平分∠ABD;③∠AOC=∠AEC;④AF=DF;⑤△CEF≌△BED;⑥BD=2OF.其中一定成立的是(请填序号)①②④⑥.
如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②CB平分∠ABD;③∠AOC=∠AEC;④AF=DF;⑤△CEF≌△BED;⑥BD=2OF.其中一定成立的是(请填序号)①②④⑥.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
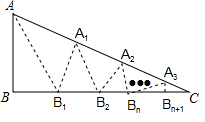 如图,在△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分…将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,则称∠BAC是△ABC的好角.
如图,在△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分…将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,则称∠BAC是△ABC的好角.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
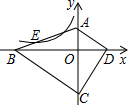 如图,四边形ABCD的顶点都在坐标轴上,若AD∥BC,△ACD与△BCD的面积分别为10和20,若双曲线y=$\frac{k}{x}$恰好经过边AB的四等分点E(BE<AE),则k的值为-$\frac{5}{2}$.
如图,四边形ABCD的顶点都在坐标轴上,若AD∥BC,△ACD与△BCD的面积分别为10和20,若双曲线y=$\frac{k}{x}$恰好经过边AB的四等分点E(BE<AE),则k的值为-$\frac{5}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com