

分析 (1)一般用增长后的量=增长前的量×(1+增长率),2016年收到微信红包金额400(1+x)万元,在2016年的基础上再增长x,就是2017年收到微信红包金额400(1+x)(1+x),由此可列出方程400(1+x)2=484,求解即可.
(2)设甜甜在2017年六一收到微信红包为y元,则她妹妹收到微信红包为(2y+34)元,根据她们共收到微信红包484元列出方程并解答.
解答 解:(1)设2015年到2017年甜甜和她妹妹在六一收到红包的年增长率是x,
依题意得:400(1+x)2=484,
解得x1=0.1=10%,x2=-2.1(舍去).
答:2015年到2017年甜甜和她妹妹在六一收到红包的年增长率是10%;
(2)设甜甜在2017年六一收到微信红包为y元,
依题意得:2y+34+y=484,
解得y=150
所以484-150=334(元).
答:甜甜在2017年六一收到微信红包为150元,则她妹妹收到微信红包为334元.
点评 本题考查了一元一次方程的应用,一元二次方程的应用.对于增长率问题,增长前的量×(1+年平均增长率)年数=增长后的量.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
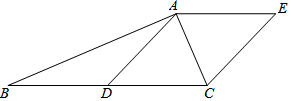 如图,Rt△ABC中,∠BAC=90°,D是BC边的中点,连接AD,过点A作AE∥BC,且AE=CD,连接EC.
如图,Rt△ABC中,∠BAC=90°,D是BC边的中点,连接AD,过点A作AE∥BC,且AE=CD,连接EC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
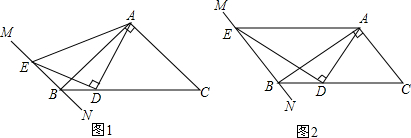
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
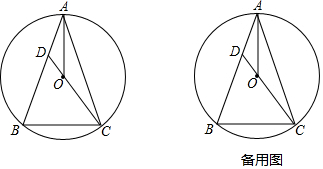
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
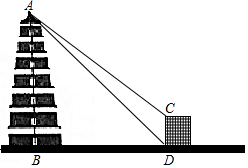 “大雁塔”是西安市的标志性建筑、著名古迹、唐代永徽三年,玄樊为藏经典而修建,塔身七层,被视为古都西安的象征.民间人士道:“不到大雁塔,不算到西安”.小明在学习了锐角三角函数后,想用所学知识测量“大雁塔”的高度,小明在一栋高15米的建筑物底部D处侧得塔顶端A的仰角为45°,接着在建筑物顶端C处测得塔顶端A的仰角为37.5°.已知AB⊥BD,CD⊥BD,请你根据题中提供的相关信息,求出“大雁塔”的高AB的长度.(结果精确到0.1米)(参考数据:sin37.5°≈0.6088,cos37.5°≈0.7934,tan37.5°≈0.7673.
“大雁塔”是西安市的标志性建筑、著名古迹、唐代永徽三年,玄樊为藏经典而修建,塔身七层,被视为古都西安的象征.民间人士道:“不到大雁塔,不算到西安”.小明在学习了锐角三角函数后,想用所学知识测量“大雁塔”的高度,小明在一栋高15米的建筑物底部D处侧得塔顶端A的仰角为45°,接着在建筑物顶端C处测得塔顶端A的仰角为37.5°.已知AB⊥BD,CD⊥BD,请你根据题中提供的相关信息,求出“大雁塔”的高AB的长度.(结果精确到0.1米)(参考数据:sin37.5°≈0.6088,cos37.5°≈0.7934,tan37.5°≈0.7673.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com