已知等腰△ABC内接于半径为5厘米的⊙O,且BC=8厘米,则△ABC的面积等于 平方厘米.
【答案】
分析:先过A作AD⊥BC于D,连接OB、OC,由于AB=AC,AD⊥BC,那么BD=CD,于是AD是BC的垂直平分线,又OB=OC,易证O在AD上,在Rt△OCD中,利用勾股定理可求OD,从而可求AD,进而可求△ABC的面积.
解答: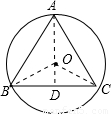
解:①如右图所示,△ABC内接于⊙O,且AB=AC,且BC=8,
过A作AD⊥BC于D,连接OB、OC,
∵AB=AC,AD⊥BC,
∴BD=CD,
∴AD是BC的垂直平分线,
又∵OB=OC,
∴点O在BC垂直平分线上,
即点O在AD上,
在Rt△OCD中,OD=
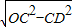
=3,
∴AD=3+5=8,
∴S
△ABC=

BC•AD=32.
②
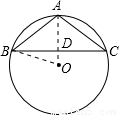
O在△ABC外时,连接OB、OA交BC于D,
由①知BD=4,AD⊥BC,
由勾股定理得:OB
2=OD
2+BD
2,
∴5
2=(5-AD)
2+4
2,
解得:AD=2,AD=8>5(舍去),
∴S
△ABC=

BC×AD=

×8×2=8,
故答案是32或8.
点评:本题考查了垂径定理、勾股定理、等腰三角形三线合一定理、垂直平分线定理及性质.解题的关键是证明O在AD上.

 解:①如右图所示,△ABC内接于⊙O,且AB=AC,且BC=8,
解:①如右图所示,△ABC内接于⊙O,且AB=AC,且BC=8,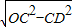 =3,
=3, BC•AD=32.
BC•AD=32. O在△ABC外时,连接OB、OA交BC于D,
O在△ABC外时,连接OB、OA交BC于D, BC×AD=
BC×AD= ×8×2=8,
×8×2=8,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案