
【题目】如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 、点
、点![]() ,
,![]() ,若将
,若将![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,折痕
重合,折痕![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 交于点
交于点![]() .
.
(1)求![]() 的值;
的值;
(2)求点![]() 的坐标;
的坐标;
(3)求直线![]() 的表达式.
的表达式.

【答案】(1) ![]() ;(2)
;(2)![]() ; (3)
; (3)![]()
【解析】
(1)先求得点B的坐标,得到![]() 2
2![]() ,再根据
,再根据![]() 角所对直角边等于斜边一半结合勾股定理即可求得
角所对直角边等于斜边一半结合勾股定理即可求得![]() 的长,从而求得答案;
的长,从而求得答案;
(2)根据折叠的性质可证得BC=AC,设![]() ,则
,则![]() ,在
,在![]() 中,利用勾股定理即可求得答案;
中,利用勾股定理即可求得答案;
(3)点D时AB的中点,则点D(3,![]() ),将点C、D的坐标代入一次函数表达式,即可求解.
),将点C、D的坐标代入一次函数表达式,即可求解.
(1)令![]() ,则
,则![]() ,即:
,即:![]() 2
2![]() ,
,
∵![]() ,
,
∴![]() 4
4![]() ,
,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
将![]() 代入
代入![]() 得:
得:![]() ,
,
∴![]() ;
;
(2)根据折叠的性质得:![]() ,
,
设![]() ,则
,则![]() ,
,
∴在![]() 中,
中,![]() ,即
,即![]() ,
,
解得:![]() ,则
,则![]() ,
,
则点C的坐标为:![]() ;
;
(3)根据折叠的性质知:点D是AB的中点,则点D的坐标为![]() ,
,
将点C、D的坐标代入一次函数的解析式![]() 得:
得: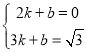 ,
,
解得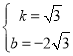 ,
,
故直线CD的表达式为:![]() .
.


科目:初中数学 来源: 题型:
【题目】已知![]() 、
、![]() 两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以每小时60千米/时的速度沿此公路从
两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以每小时60千米/时的速度沿此公路从![]() 地匀速开往
地匀速开往![]() 地,乙车从
地,乙车从![]() 地沿此公路匀速开往
地沿此公路匀速开往![]() 地,两车分别到达目的地后停止甲、乙两车相距的路程
地,两车分别到达目的地后停止甲、乙两车相距的路程![]() (千米)与甲车的行驶时间
(千米)与甲车的行驶时间![]() (时)之间的函数关系如图所示:
(时)之间的函数关系如图所示:
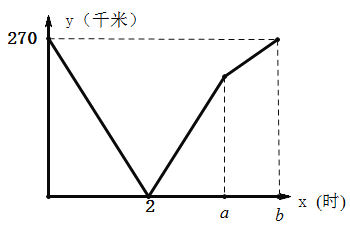
(1)乙年的速度为______千米/时,![]() _____,
_____,![]() ______.
______.
(2)求甲、乙两车相遇后![]() 与
与![]() 之间的函数关系式,并写出相应的自变量
之间的函数关系式,并写出相应的自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件30元,售价为每件40元.每天可以销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;
(2)经调查,若每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
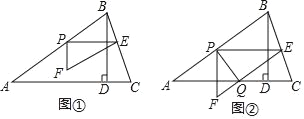
【题目】如图①,在锐角△ABC中,AB=5,tanC=3,BD⊥AC于点D,BD=3,点P从点A出发,以每秒1个单位长度的速度沿AB向终点B运动,过点P作PE∥AC交边BC于点E,以PE为边作Rt△PEF,使∠EPF=90°,点F在点P的下方,且EF∥AB.设△PEF与△ABD重叠部分图形的面积为S(平方单位)(S>0),点P的运动时间为t(秒)(t>0).
(1)求线段AC的长.
(2)当△PEF与△ABD重叠部分图形为四边形时,求S与t之间的函数关系式.
(3)若边EF与边AC交于点Q,连结PQ,如图②.
①当PQ将△PEF的面积分成1:2两部分时,求AP的长.
②直接写出PQ的垂直平分线经过△ABC的顶点时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形ABCDEF中,P、Q两点分别为△ACF、△CEF的内心.若AF=2,则PQ的长度为何?( )
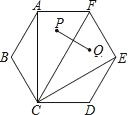
A. 1 B. 2 C. 2![]() ﹣2 D. 4﹣2
﹣2 D. 4﹣2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某共享单车公司提供了手机和会员卡两种支付方式.若用手机支付方式,骑行时间在半小时以内(含半小时)不收费,超出半小时后每半小时收费1元,若选择会员卡支付,骑行时间每半小时收费0.8元,设骑行时间为x小时.
(1)根据题意,填写下表(单位:元):
骑行时间(小时) | 0.5 | 2 | 3 | … |
手机支付付款金额(元) | 0 | … | ||
会员卡支付付款金额(元) | 3.2 | … |
(2)设用手机支付付款金额为y1元,用会员卡支付付款金额为y2元,分别写出y1,y2关于x的函数关系式;
(3)若李老师经常骑行该公司的共享单车,他应选择哪种支付方式比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
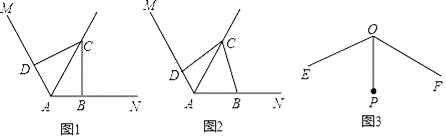
【题目】已知∠MAN=120°,点C是∠MAN的平分线AQ上的一个定点,点B,D分别在AN,AM上,连接BD.
【发现】
(1)如图1,若∠ABC=∠ADC=90°,则∠BCD= °,△CBD是 三角形;
【探索】
(2)如图2,若∠ABC+∠ADC=180°,请判断△CBD的形状,并证明你的结论;
【应用】
(3)如图3,已知∠EOF=120°,OP平分∠EOF,且OP=1,若点G,H分别在射线OE,OF上,且△PGH为等边三角形,则满足上述条件的△PGH的个数一共有 .(只填序号)
①2个②3个③4个④4个以上
查看答案和解析>>
科目:初中数学 来源: 题型:
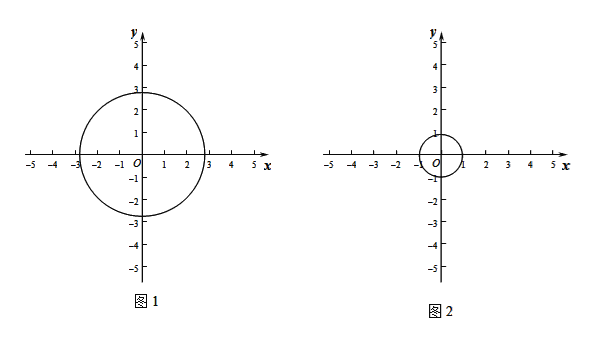
【题目】在平面直角坐标系中,定义点P(x,y)的变换点为P′(x+y,x﹣y).
(1)如图1,如果⊙O的半径为2![]() ,
,
①判断M(2,0),N(﹣2,1)两个点的变换点M′、N′与⊙O的位置关系;
②若点P在直线y=x-2上,点P的变换点P′不在⊙O外,结合图形求点P横坐标x的取值范围.
(2)如图2,如果⊙O的半径为1,且P的变换点P′在直线y=﹣2x+5上,求点P与⊙O上任意一点距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com