
 如图,在某段测速公路BC上(公路视为直线)交通管理部门规定汽车的最高行驶速度不能超过60千米/时,并在离该公路100米处设置了一个监测点A,已知点B在A的北偏西60°方向上,点C在点A的偏东40°方向上.(1)监测发现,一辆汽车从点B匀速行驶到点C所用时间为15秒.请你通过计算,判断该越野车在这段限速路上是否超速?(参考数据:sin40°=0.64,tan40°=0.84,$\sqrt{3}$=1.73)
如图,在某段测速公路BC上(公路视为直线)交通管理部门规定汽车的最高行驶速度不能超过60千米/时,并在离该公路100米处设置了一个监测点A,已知点B在A的北偏西60°方向上,点C在点A的偏东40°方向上.(1)监测发现,一辆汽车从点B匀速行驶到点C所用时间为15秒.请你通过计算,判断该越野车在这段限速路上是否超速?(参考数据:sin40°=0.64,tan40°=0.84,$\sqrt{3}$=1.73)分析 (1)过点A作AD⊥BC于点D,通过解直角三角形求出BD、CD的长,再根据速度=路程÷时间即可求出越野车的速度,由此即可得出结论;
(2)先求出小汽车的速度,再根据时间=路程÷速度和,即可求出两车相遇的时间.
解答 解:(1)过点A作AD⊥BC于点D,如图所示.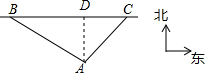
由已知得:AD=100,∠BAD=60°,∠CAD=40°,
∴BD=AD•tan∠BAD=173,CD=AD•tan∠CAD=84,
∴BC=BD+CD=257.
该越野车的速度为:257÷15×3.6=61.68(千米/时),
∵61.68>60,
∴该越野车在这段限速路上超速行驶了.
(2)小汽车的速度为:15×$\frac{4}{3}$=20(米/秒),
两车相遇的时间为:257÷(15+20)≈7.34(秒).
答:经过大约7.34秒两车相遇.
点评 本题考查了解直角三角形的应用中的方向角问题,解题的关键是:(1)求出线段BC的长度;(2)根据数量关系求出相遇时间.本题属于中档题,难度不大,解决该题型题目时,构建直角三角形通过解直角三角形求出边角是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 总体是240 | B. | 样本容量是60 | C. | 样本是60名学生 | D. | 个体是每个学生 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-2>b-2 | B. | a+2>b+2 | C. | $\frac{1}{2}$a>$\frac{1}{2}$b | D. | -2a>-2b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | $\sqrt{4\frac{1}{4}}$=2$\frac{1}{2}$ | D. | $\sqrt{(-3)^{2}}$=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1,2,3 | B. | $\sqrt{2}$,$\sqrt{3}$,5 | C. | 5,6,7 | D. | 0.3,0.4,0.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).
如图,三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com