
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完成:
(1)化简函数解析式,当![]() 时,
时,![]() ___________,当
___________,当![]() 时
时![]() ____________;
____________;
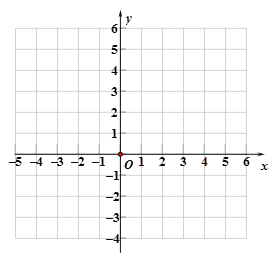
(2)根据(1)中的结果,请在所给坐标系中画出函数![]() 的图象;备用图
的图象;备用图
(3)结合画出的函数图象,解决问题:若关于![]() 的方程
的方程![]() 只有一个实数根,直接写出实数
只有一个实数根,直接写出实数![]() 的取值范围:___________________________.
的取值范围:___________________________.
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】“六一”儿童节前夕,某县教育局准备给留守儿童赠送一批学习用品,先对红星小学的留守儿童人数进行抽样统计,发现各班留守儿童人数分别为6名,7名,8名,10名,12名这五种情形,并绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
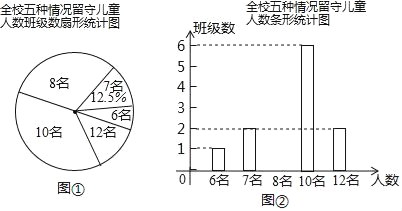
(1)该校有_____个班级,补全条形统计图;
(2)求该校各班留守儿童人数数据的平均数,众数与中位数;
(3)若该镇所有小学共有60个教学班,请根据样本数据,估计该镇小学生中,共有多少名留守儿童.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c(b,c是常数)与x轴相交于A,B两点(A在B的左侧),与y轴交于点C.
(1)当A(﹣1,0),C(0,﹣3)时,求抛物线的解析式和顶点坐标;
(2)P(m,t)为抛物线上的一个动点.
①当点P关于原点的对称点P′落在直线BC上时,求m的值;
②当点P关于原点的对称点P′落在第一象限内,P′A2取得最小值时,求m的值及这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像分别与
的图像分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,以线段
,以线段![]() 为边在第四象限内作等腰直角
为边在第四象限内作等腰直角![]() ,且
,且![]() .
.
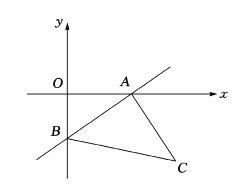
(1)试写出点![]() 的坐标:
的坐标: ![]() (_ _,_ ___),
(_ _,_ ___),![]() (_ ,_ )
(_ ,_ )
(2)求点![]() 的坐标;
的坐标;
(3)求直线![]() 的函数表达式
的函数表达式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,BD=CE,将线段AE沿AC翻折,得到线段AM,连结EM交AC于点N,连结DM、CM以下说法:①AD=AM,②∠MCA=60°,③CM=2CN,④MA=DM中,正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0;②a+b+c>0;③方程ax2+bx+c=0的根是x1=﹣1,x2=3; ④b2﹣4ac>0;⑤当x>1时,y随x的增大而增大;正确的说法有( )
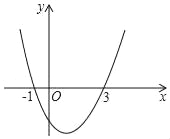
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
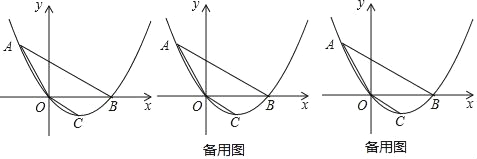
【题目】如图,顶点为C的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,连接OC、OA、AB,已知OA=OB=2,∠AOB=120°.
(1)求这条抛物线的表达式;
(2)过点C作CE⊥OB,垂足为E,点P为y轴上的动点,若以O、C、P为顶点的三角形与△AOE相似,求点P的坐标;
(3)若将(2)的线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<120°),连接E′A、E′B,求E′A+![]() E′B的最小值.
E′B的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com