
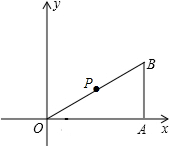
 己知:Rt△OAB在直角坐标系中的位置如图所示,点B的坐标为(4,2),P为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分,问:点C在什么位置时,分割得到的三角形与Rt△OAB相似?要求在图上画出所有符合要求的线段PC,并求出相应的点C的坐标.
己知:Rt△OAB在直角坐标系中的位置如图所示,点B的坐标为(4,2),P为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分,问:点C在什么位置时,分割得到的三角形与Rt△OAB相似?要求在图上画出所有符合要求的线段PC,并求出相应的点C的坐标. 分析 由于C点不确定,故分△OPC∽△OBA,△BPC∽△BOA,△OPC∽△OAB三种情况进行讨论.
解答 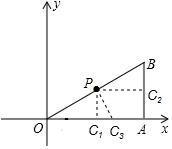 解:∵点B的坐标为(4,2),
解:∵点B的坐标为(4,2),
∴OA=4,AB=2,OB=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,OP=$\sqrt{5}$.
如图,当△OPC∽△OBA时,
∵$\frac{OC}{OA}$=$\frac{OP}{OB}$=$\frac{1}{2}$,即$\frac{PC}{2}$=$\frac{OC}{4}$=$\frac{1}{2}$,
∴PC=1,OC=2,
∴C1(2,0);
当△BPC∽△BOA时,
∵$\frac{PB}{OB}$=$\frac{BC}{OA}$=$\frac{PC}{OA}$,即$\frac{1}{2}$=$\frac{BC}{2}$=$\frac{PC}{4}$,解得BC=2,
∴AC=1-1=1,
∴C2(4,1);
当△OPC∽△OAB时,
∴$\frac{OP}{OA}$=$\frac{OC}{OB}$,即$\frac{\sqrt{5}}{4}$=$\frac{OC}{2\sqrt{5}}$,解得OC=2.5,
∴C3(2.5,0);
综上所述,C点坐标为:(2,0)或(4,1)或(2.5,0).
点评 本题考查的是相似三角形的判定,在解答此题时要注意进行分类讨论,不要漏解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{15}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 14 | B. | 7 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,点M是BC边上任意一点,请你仅用无刻度直尺,用连线的方法,在图中按要求作图(保留作图痕迹,不写作法),在AB边上求一点N,连接CN,使CN=AM,并说明理由.
如图,在正方形ABCD中,点M是BC边上任意一点,请你仅用无刻度直尺,用连线的方法,在图中按要求作图(保留作图痕迹,不写作法),在AB边上求一点N,连接CN,使CN=AM,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com