练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，正方形ABCD的边长为6，E为BC上的一点，BE=2，F为AB上的一点，AF=3，P为AC上一点，则PF+PE的最小值为 ．

    【答案】
    【解析】解：作E关于直线AC的对称点E′，连接E′F，则E′F即为所求，

    过F作FG⊥CD于G，
    在Rt△E′FG中，
    GE′=CD﹣BE﹣BF=6﹣2﹣3=1，GF=6，
    所以E′F= ．
    所以答案是： ．
    【考点精析】解答此题的关键在于理解正方形的性质的相关知识，掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】“五一节”期间，小明一家自驾游去了离家240千米的某地，如图是他们离家的距离y（千米）与汽车行驶时间x（小时）之间的函数图象．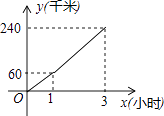

    （1）求出y（千米）与x（小时）之间的函数表达式；
    （2）他们出发2小时时，离目的地还有多少千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”，它是用八个全等的直角三角形拼接而成，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3．若S1+S2+S3＝15，则S2的值是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如上图所示．已知：在正方形ABCD中，∠BAC的平分线交BC于E，作EF⊥AC于F，作FG⊥AB于G．则 = ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点O是矩形ABCD的中心，E是AB上的点，沿CE折叠后，点B恰好与点O重合，若BC=3，则折痕CE的长为（ ）

    A.2
    B.
    C.
    D.6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为了了解初三年级1000名学生的身体健康情况，从该年级随机抽取了若干名学生，将他们按体重（均为整数，单位：kg）分成五组（A：39.5～46.5；B：46.5～53.5；C：53.5～60.5；D：60.5～67.5；E：67.5～74.5），并依据统计数据绘制了如下两幅尚不完整的统计图．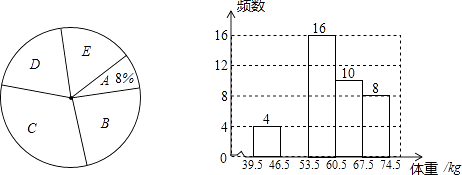

    解答下列问题：
    （1）这次抽样调查的样本容量是 ， 并补全频数分布直方图；
    （2）C组学生的频率为 ， 在扇形统计图中D组的圆心角是度；
    （3）请你估计该校初三年级体重超过60kg的学生大约有多少名？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把下列各式分解因式：
    （1）3x﹣12x3
    （2）（x2+4）2﹣16x2
    （3）y（y+4）﹣4（y+1）
    （4）
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC是等边三角形，点D是直线BC上一点，以AD为一边在AD的右侧作等边△ADE.

    (1)如图①，点D在线段BC上移动时，直接写出∠BAD和∠CAE的大小关系；

    (2)如图②，点D在线段BC的延长线上移动时，猜想∠DCE的大小是否发生变化．若不变请求出其大小；若变化，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】认真阅读下面关于三角形内外角平分线的研究片断，完成所提出的问题.

    探究1：如图(1)在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现∠BOC=90°+∠A，理由如下：

    ∵BO和CO分别是∠ABC和∠ACB的角平分线，∴∠1=∠ABC，∠2=∠ACB.

    ∴∠1+∠2= (∠ABC+∠ACB)= (180°－∠A)=90°－∠A.

    ∴∠BOC=180°－(∠1+∠2)=180°－(90°－∠A)=90°+∠A

    探究2：如图(2)中，O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？请说明理由.

    查看答案和解析>>

    同步练习册答案