
 .
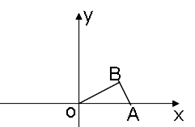
. ,利用正弦的定义得sin∠BOA=
,利用正弦的定义得sin∠BOA= ,则∠BOA=30°,设该三角形绕着点O逆时针旋转120°后点B的对应点为B′,根据旋转的性质得∠BOB′=120°,则OB′与x轴的负半轴的夹角为30°,且OB′=OB=2
,则∠BOA=30°,设该三角形绕着点O逆时针旋转120°后点B的对应点为B′,根据旋转的性质得∠BOB′=120°,则OB′与x轴的负半轴的夹角为30°,且OB′=OB=2 ,作B′H⊥x轴,在Rt△OB′H中,根据含30度的直角三角形三边的关系得B′H=
,作B′H⊥x轴,在Rt△OB′H中,根据含30度的直角三角形三边的关系得B′H=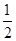 OB′=
OB′= ,OH=
,OH= B′H=3,所以B′点的坐标为(-3,
B′H=3,所以B′点的坐标为(-3, ),设点B′所落在的反比例函数解析式为y=
),设点B′所落在的反比例函数解析式为y= ,利用反比例函数图象上点的坐标特征得到k-3
,利用反比例函数图象上点的坐标特征得到k-3 ,从而得到该反比例函数的解析式为
,从而得到该反比例函数的解析式为 .
.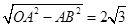 ,
, ,
, ,
,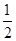 OB′=
OB′= ,OH=
,OH= B′H=3,
B′H=3, ),
), ,
, =-3
=-3
 .
.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源:不详 题型:解答题
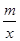 的图象经过点C.
的图象经过点C.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

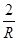 B.I=
B.I=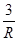
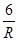 D.I=-
D.I=-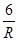
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com