
【题目】如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=13,BC=15,CA=14,则tan∠EDF的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
由切线长定理可求AF=AE=6,BF=BD=7,CD=CE=8,由勾股定理可得AM=11.2,由三角形面积公式可求EO=4,由圆周角定理可求∠AOE=∠EDF,即可求解.
解:如图,过点A作AM⊥BC,连接AO,BO,CO,EO,FO,DO,
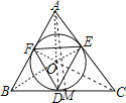
∴EO⊥AC,FO⊥AB,DO⊥BC,OF=OE=OD,
∵△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,
∴AF=AE,BF=BD,CD=CE,
∵AF+BF=AB=13,BD+CD=BC=15,AE+CE=AC=14
∴AF=AE=6,BF=BD=7,CD=CE=8
∵AB2-BM2=AM2,AC2-MC2=AM2,
∴BM=6.6,AM=11.2,
∵S△ABC=S△ABO+S△BCO+S△ACO,
∴![]() ×BC×AM=
×BC×AM=![]() ×AB×FO+
×AB×FO+![]() ×AC×OE+
×AC×OE+![]() ×BC×OD,
×BC×OD,
∴15×11.2=13EO+14EO+15EO
∴EO=4
∵∠EOF=2∠EDF
∴∠AOE=∠EDF
∴tan∠EDF=tan∠AOE=![]() =
=![]()
故选:B.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C(0,3),且OB=OC=3AO.直线y=x+1与抛物线交于A、D两点,与y轴交于点E,点Q是抛物线的顶点,设直线AD上方的抛物线上的动点P的横坐标为m.
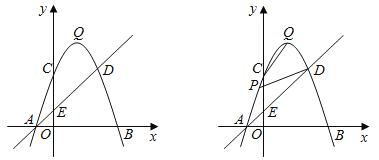
(1)求该抛物线的解析式及顶点Q的坐标;
(2)连结CQ,判断线段CQ与线段AE的数量关系和位置关系,并说明理由.
(3)连结PA、PD,当m为何值时,S△PAD=![]() S△DAB;
S△DAB;
(4)在直线AD上是否存在一点H使△PQH为等腰直角三角形,若存在请求出m的值,不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
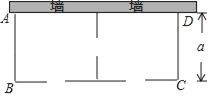
【题目】某农场要建一个饲养场(长方形ABCD),饲养场的一面靠墙(墙最大可用长度为27米),另三边用木栏围成,中间也用木栏隔开,分成两个场地,并在如图所示的三处各留1米宽的门(不用木栏),建成后木栏总长57米,设饲养场(长方形ABCD)的宽为a米.
(1)饲养场的长为多少米(用含a的代数式表示).
(2)若饲养场的面积为288m2,求a的值.
(3)当a为何值时,饲养场的面积最大,此时饲养场达到的最大面积为多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
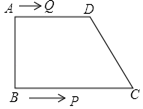
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发以
出发以![]() 的速度向点
的速度向点![]() 运动,点
运动,点![]() 从点
从点![]() 出发以
出发以![]() 的速度向
的速度向![]() 点运动,
点运动,![]() 、
、![]() 两点同时出发,其中一点到达终点时另一点也停止运动.若
两点同时出发,其中一点到达终点时另一点也停止运动.若![]() ,当
,当![]() __
__![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】童老师计划购买A、B两种笔记本共30本作为班会奖品,这两种笔记本的单价分别是12元和8元,并且购买的A种笔记本的数量要少于B种笔记本数量的![]() ,但又不少于B种笔记本数量的
,但又不少于B种笔记本数量的![]() .如果设买A种笔记本x本,买这两种笔记本共花费y元.
.如果设买A种笔记本x本,买这两种笔记本共花费y元.
(1)求计划购买这两种笔记本所需的费用y(元)关于x(本)的函数关系式;
(2)童老师有多少种不同的购买方案?
(3)商店为了促销,决定对A种笔记本每本让利a(4<a≤7)元销售,B种笔记本每本让利b元销售,童老师发现购买所需的总费用与购买的方案无关.当总费用最少时,求此时a、b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点D是△ABC中AC的中点,AE∥BC,ED交AB于点G,交BC的延长线于点F.
(1)求证:△GAE∽△GBF;
(2)求证:AE=CF;
(3)若BG:GA=3:1,BC=8,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①ac<0,②b﹣2a<0,③b2﹣4ac<0,④a﹣b+c<0,正确的是( )
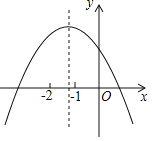
A.①②B.①④C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山东省烟台市)某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
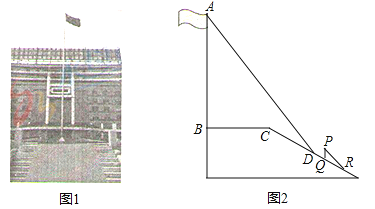
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com