
分析 分两种情况考虑:当两条弦位于圆心O一侧时,如图1所示,过O作OE⊥CD,交CD于点E,交AB于点F,连接OA,OC,由AB∥CD,得到OE⊥AB,利用垂径定理得到E与F分别为CD与AB的中点,在直角三角形AOF中,利用勾股定理求出OF的长,在三角形COE中,利用勾股定理求出OE的长,由OE-OF即可求出EF的长;当两条弦位于圆心O两侧时,如图2所示,同理由OE+OF求出EF的长即可.
解答 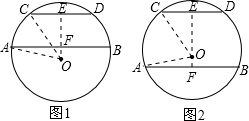 解:分两种情况考虑:
解:分两种情况考虑:
当两条弦位于圆心O一侧时,如图1所示,
过O作OF⊥AB,交AB于点F,交CD于点E,连接OA,OC,
∵AB∥CD,∴OE⊥CD,
∴F、E分别为AB、CD的中点,
∴AF=BF=$\frac{1}{2}$AB=4,CE=DE=$\frac{1}{2}$CD=3,
在Rt△COE中,OC=5,CE=3,
根据勾股定理得:OE=4,
在Rt△AOF中,OA=5,AF=4,
根据勾股定理得:OF═3,
则EF=OE-OF=4-3=1;
当两条弦位于圆心O两侧时,如图2所示,同理可得EF=4+3=7,
综上,弦AB与CD的距离为7或1.
故答案为:7或1.
点评 此题考查了垂径定理,勾股定理,利用了分类讨论的思想,熟练掌握垂径定理是解本题的关键.


科目:初中数学 来源: 题型:解答题
 小军同学拿着边长为acm的等边三角形硬纸片从图示的位置开始在数轴上顺时针无滑动地向右滚动,当三角形的一个顶点落在x=b处时,停止滚动,且(a-1)2+|b-5|=0.
小军同学拿着边长为acm的等边三角形硬纸片从图示的位置开始在数轴上顺时针无滑动地向右滚动,当三角形的一个顶点落在x=b处时,停止滚动,且(a-1)2+|b-5|=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC三个顶点的坐标分别为A(-1,3),B(-4,1),C(-2,1).
如图,△ABC三个顶点的坐标分别为A(-1,3),B(-4,1),C(-2,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com