
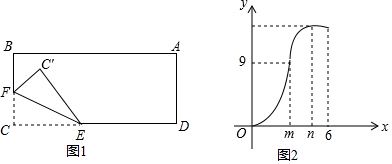
分析 (1)根据三角形面积公式即可得到答案.
(2)分三种情形讨论①0<t≤3,此时s=S△EFC②3<t≤$\frac{24}{5}$,此时s=S四边形EFNK③$\frac{24}{5}$<t≤7,此时s=S△ENK.
解答 解:(1)由题意$\frac{1}{2}$•t•2t=9,
解得t=3(或-3舍弃),
∴m=3,
故答案为3.
(2)当0<t≤3时,s=S△EFC′=$\frac{1}{2}$•t•2t=t2,
当t=3时,如图1、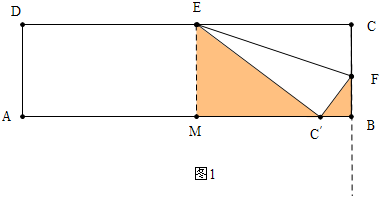 ,
,
由题意CF=FC′=3,EC=6,作EM⊥AB垂足为M,设BF=x,
∵∠EMB=∠MBC=∠C=90°,
∴四边形EMBC是矩形,
∴EC=BM=6,EM=BC=3+x,EC=EC′=6,
∵∠E′CM+′FC′B=90°,∠FC′B+′C′FB=90°,
∴∠ECM=∠C′FB,
∴△EC′M∽△C′FB,
∴$\frac{EC′}{C′F}$=$\frac{EM}{BC′}$,
∴$\frac{6}{3}$=$\frac{3+x}{\sqrt{9-{x}^{2}}}$,
解得x=$\frac{9}{5}$,
∴BC=$\frac{24}{5}$
∴当3<t≤$\frac{24}{5}$时,如图2 ,
,
作EM⊥AB垂足为M,
由(1)可知在Rt△EMK中,∵EM=BC=$\frac{24}{5}$,EK=6,
∴MK=$\frac{18}{5}$,
∵∠FNB=∠KNC′,∠KNC′+∠C′KN=90°,∠NKC′=′EKM,∠MEK+∠EKM=90°,
∴∠FNB=∠MEK,
∵∠EMK=∠FBN=90°,
∴△EMK∽△NBF,
∴$\frac{EK}{NF}$$\frac{MK}{FB}$,
∴$\frac{6}{FN}$=$\frac{\frac{18}{5}}{\frac{24}{5}-t}$,
∴FN=$\frac{5}{3}$($\frac{24}{5}$-t),NC′=FC′-NF=t-$\frac{5}{3}$($\frac{24}{5}$-t),
∵∠EMK=∠C′=90°,∠EKM=∠NKC′,
∴△EMK∽△CNK,
∴$\frac{EM}{C′N}$=$\frac{MK}{C′K}$,
∴$\frac{\frac{24}{5}}{t-\frac{5}{3}(\frac{24}{5}-t)}$=$\frac{\frac{18}{5}}{C′K}$
∴C′K=$\frac{3}{4}$[t-$\frac{5}{3}$($\frac{24}{5}$-t)],
∴s=S四边形EFNK=S△EFC′-S△KNC′=t2-$\frac{1}{2}$•$\frac{3}{4}$[t-$\frac{5}{3}$($\frac{24}{5}$-t)]2=-$\frac{5}{3}$t2+16t-24.
当$\frac{24}{5}$<t≤7时,如图3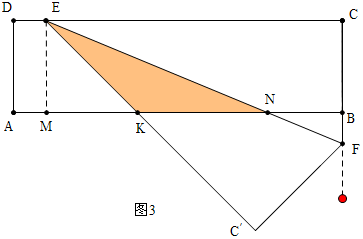 ,
,
∵∠CEN=∠NEK=∠ENK,
∴EK=KN=6,
∴s=S△ENK=$\frac{1}{2}$•KN•EM=$\frac{1}{2}$•KN•EM=$\frac{1}{2}$×6×$\frac{24}{4}$=$\frac{72}{5}$.
综上所述:s=$\left\{\begin{array}{l}{{t}^{2}(0<t≤3)}\\{-\frac{5}{3}{t}^{2}+16t-24(3<t≤\frac{24}{5})}\\{\frac{72}{5}(\frac{24}{5}<t≤7)}\end{array}\right.$.
点评 本题考查翻折变换的有关性质、勾股定理、相似三角形的判定和性质、重叠部分面积的计算,正确画出图形确定变量t的取值范围是解决问题的关键.


科目:初中数学 来源: 题型:解答题
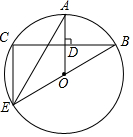 如图,BE是⊙O的直径,半径OA⊥弦BC,点D为垂足,连AE,EC.
如图,BE是⊙O的直径,半径OA⊥弦BC,点D为垂足,连AE,EC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有趣的问题,太准了!
有趣的问题,太准了!查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平行四边形ABCD中,点E为DC上一点,连接AE,F为AE上一点,连接BF,∠AFB=∠EFB,G在BF上,连接AG、EG,FG平分∠AGE.
如图,平行四边形ABCD中,点E为DC上一点,连接AE,F为AE上一点,连接BF,∠AFB=∠EFB,G在BF上,连接AG、EG,FG平分∠AGE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
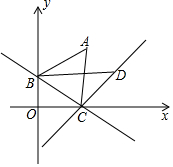 如图,直线y=-$\frac{\sqrt{3}}{3}$x+2与x轴交于点C,与y轴交于点B,点A在第一象限内,△ABC是正三角形,点D是直线y=x-2$\sqrt{3}$上第一象限内一点,△DBC和△ABC面积相等,则点D的坐标是(6,6-2$\sqrt{3}$).
如图,直线y=-$\frac{\sqrt{3}}{3}$x+2与x轴交于点C,与y轴交于点B,点A在第一象限内,△ABC是正三角形,点D是直线y=x-2$\sqrt{3}$上第一象限内一点,△DBC和△ABC面积相等,则点D的坐标是(6,6-2$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com