
【题目】补全解答过程:
已知:如图,直线![]() ,直线
,直线![]() 与直线
与直线![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() ;
;![]() 平分
平分![]() ,
,![]() .求
.求![]() 的度数.
的度数.

解:![]() 与
与![]() 交于点
交于点![]() ,(已知)
,(已知)
![]() .(_______________)
.(_______________)
![]() ,(已知)
,(已知)
![]() .(______________)
.(______________)
![]() ,
,![]() 与
与![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,(已知)
,(已知)
![]() (_____________)
(_____________)
![]() _______
_______![]()
![]() 平分
平分![]() ,(已知)
,(已知)
![]() _______
_______![]() .(角平分线的定义)
.(角平分线的定义)
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程
如图,点A,O,B在同一条直线上, OD,OE分别平分∠AOC和∠BOC.

(1)求∠DOE的度数;
(2)如果∠COD=65°,求∠AOE的度数.
解:(1)如图,因为OD是∠AOC的平分线,
所以∠COD =![]() ∠AOC.
∠AOC.
因为OE是∠BOC 的平分线,
所以 =![]() ∠BOC.
∠BOC.
所以∠DOE=∠COD+ =![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB= °.
∠AOB= °.
(2)由(1)可知∠BOE=∠COE = -∠COD= °.
所以∠AOE= -∠BOE = °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )
A.①②
B.②③
C.①③
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于点P(a,b),点Q(c,d),如果a﹣b=c﹣d,那么点P与点Q就叫作等差点.例如:点P(4,2),点Q(﹣1,﹣3),因4﹣2=1﹣(﹣3)=2,则点P与点Q就是等差点.如图在矩形GHMN中,点H(2,3),点N(﹣2,﹣3),MN⊥y轴,HM⊥x轴,点P是直线y=x+b上的任意一点(点P不在矩形的边上),若矩形GHMN的边上存在两个点与点P是等差点,则b的取值范围为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
(1)若![]() ,则
,则![]() 的度数为______;
的度数为______;
(2)若![]() ,直线
,直线![]() 经过点
经过点![]() .
.
①如图2,若![]() ,求
,求![]() 的度数(用含
的度数(用含![]() 的代数式表示);
的代数式表示);
②如图3,若![]() 绕点
绕点![]() 旋转,分别交线段
旋转,分别交线段![]() 于点
于点![]() ,试问在旋转过程中
,试问在旋转过程中![]() 的度数是否会发生改变?若不变,求出
的度数是否会发生改变?若不变,求出![]() 的度数(用含
的度数(用含![]() 的代数式表示),若改变,请说明理由:
的代数式表示),若改变,请说明理由:
③如图4,继续旋转直线![]() ,与线段
,与线段![]() 交于点
交于点![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,请直接写出
,请直接写出![]() 与
与![]() 的关系(用含
的关系(用含![]() 的代数式表示).
的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是菱形,在平面直角坐标系中的位置如图,边AD经过原点O,已知A(0,﹣3),B(4,0),反比例函数图象经过点C,直线AC交双曲线另一支于点E,连接DE,CD,设反比例函数解析式为y1= ![]() ,直线AC解析式为y2=ax+b.
,直线AC解析式为y2=ax+b.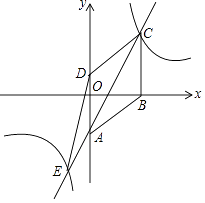
(1)求反比例函数解析式;
(2)当y1<y2时,求x的取值范围;
(3)求△CDE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com