
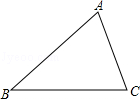
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
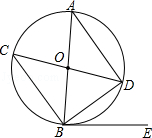
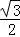 ,求此圆直径.
,求此圆直径.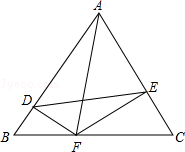
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
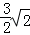 ,试求点F的坐标.
,试求点F的坐标.
|
|
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
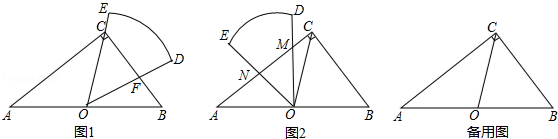
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
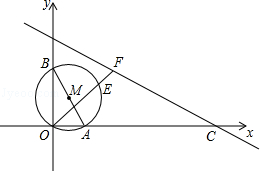
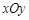 中,对于⊙A上一点B及⊙A外一点P,给出如下定义:若直线PB与 x轴有公共点(记作M),则称直线PB为⊙A的“x关联直线”,记作
中,对于⊙A上一点B及⊙A外一点P,给出如下定义:若直线PB与 x轴有公共点(记作M),则称直线PB为⊙A的“x关联直线”,记作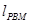 .
.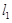 :
: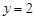 ,直线
,直线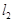 :
: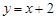 ,直线
,直线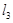 :
: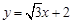 ,直线
,直线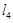 :
: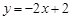 都经过点P,在直线
都经过点P,在直线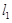 ,
, 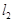 ,
, 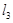 ,
, 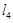 中,是⊙O的“x关联直线”的是 ;
中,是⊙O的“x关联直线”的是 ;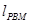 是⊙O的“x关联直线”,则点M的横坐标
是⊙O的“x关联直线”,则点M的横坐标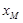 的最大值是 ;
的最大值是 ;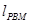 :
: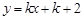 ,点M的横坐标为
,点M的横坐标为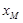 ,当
,当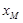 最大时,求k的值;
最大时,求k的值; 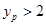 ,⊙A的两条“x关联直线”
,⊙A的两条“x关联直线”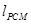 ,
,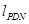 是⊙A的两条切线,切点分别为C,D,作直线CD与x轴点于点E,当点P的位置发生变化时, AE的长度是否发生改变?并说明理由.
是⊙A的两条切线,切点分别为C,D,作直线CD与x轴点于点E,当点P的位置发生变化时, AE的长度是否发生改变?并说明理由.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
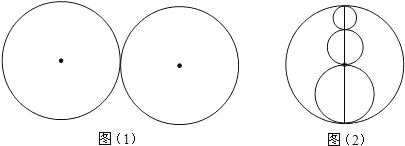 外圆的直径不变,喷水池边沿的宽度、高度不变,你认为砌喷水池的边沿( )
外圆的直径不变,喷水池边沿的宽度、高度不变,你认为砌喷水池的边沿( )| A.图(1)需要的材料多 |
| B.图(2)需要的材料多 |
| C.图(1)、图(2)需要的材料一样多 |
| D.无法确定 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
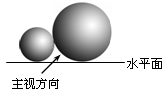
| A.两个外离的圆 | B.两个外切的圆 |
| C.两个相交的圆 | D.两个内切的圆 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com